题目内容
设f(x)=ax+b,且
[f(x)]2dx=1,求f(a)的取值范围.
| ∫ | 1 -1 |
考点:定积分
专题:导数的概念及应用
分析:先根据定积分求出a与b的关系,再根据函数的单调性求函数值得值域.
解答:
解:∵f(x)=ax+b,且
[f(x)]2dx=1,
∴
(a2x2+2abx+b2)dx=(
a2x3+abx2+b2x)|
=(
a2+ab+b2)-(-
a2+ab-b2)=
a2+2b2=1,
∴a2=
-3b2,且
-3b2≥0,即-
≤b≤
,
∴f(a)=a2+b=
-3b2+b=-3(b-
)2+
,
∴函数f(b)在[-
,
)上单调递增,在[
,
]上单调递减,
∴f(b)的最大值为f(
)=
,f(b)的最小值为f(-
)=-
,
∴f(a)的取值范围为[-
,
].
| ∫ | 1 -1 |
∴
| ∫ | 1 -1 |
| 1 |
| 3 |
1 -1 |
| 1 |
| 3 |
| 1 |
| 3 |
| 2 |
| 3 |
∴a2=
| 3 |
| 2 |
| 3 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴f(a)=a2+b=
| 3 |
| 2 |
| 1 |
| 2 |
| 9 |
| 4 |
∴函数f(b)在[-
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴f(b)的最大值为f(
| 1 |
| 2 |
| 9 |
| 4 |
| ||
| 2 |
| ||
| 2 |
∴f(a)的取值范围为[-
| ||
| 2 |
| 9 |
| 4 |
点评:本题考查了定积分的计算以及二次函数的图象和性质,属于中档题.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
ρ=
(cosθ-sinθ)(ρ>0)的圆心极坐标为( )
| 2 |
A、(-1,
| ||||
B、(1,
| ||||
C、(
| ||||
D、(1,
|
在定义域内满足f(x)•f(y)=f(x+y)的函数为( )
| A、f(x)=kx(k≠0) |
| B、f(x)=ax(a>0且a≠1) |
| C、f(x)=logax(a>0且a≠1) |
| D、f(x)=ax2+bx+c(a≠0) |
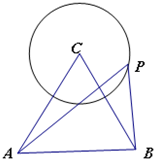 如图,△ABC是边长为2
如图,△ABC是边长为2