题目内容
3.已知命题p:?x>1,x2-2x+1>0,则¬p是假命题(真命题/假命题).分析 根据已知中的原命题,结合全称命题否定的方法,写出原命题的否定,进而可得答案.
解答 解:∵命题p:?x>1,x2-2x+1>0,
∴¬p:?x>1,x2-2x+1≤0,
由x2-2x+1=(x-1)2>0在x>1时,恒成立,
故¬p为假命题,
故答案为:假命题
点评 本题考查的知识点是命题的否定,全称命题,难度不大,属于基础题.

练习册系列答案
相关题目
13.执行如图的程序框图,则输出S的值为( )
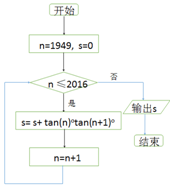

| A. | $\frac{tan2017°-tan1949°}{tan1°}$-67 | B. | $\frac{tan2016°-tan1949°}{tan1°}$-67 | ||
| C. | $\frac{tan2017°-tan1949°}{tan1°}$-68 | D. | $\frac{tan2016°-tan1949°}{tan1°}$-68 |
14.若不等式 $m>n与\frac{1}{m}>\frac{1}{n}(m,n∈R)$ 同时成立,则 ( )
| A. | m>0>n | B. | 0>m>n | ||
| C. | m>n>0 | D. | m,n与0的大小关系不确定 |
8.已知双曲线$\frac{{y}^{2}}{{a}^{2}}$-$\frac{{x}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线平行于直线l:y=x+10,双曲线的一个焦点在直线l上,则双曲线的方程为( )
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | y2-x2=50 | D. | x2-y2=10 |
5.不等式(x+1)(x-2)>0的解集为( )
| A. | {x|x<-1或x>2} | B. | {x|x<-2或x>1} | C. | {x|-2<x<1} | D. | {x|-1<x<2} |
6.近年来我国电子商务行业迎来发展的新机遇.2016年双十一期间,某购物平台的销售业绩高达516亿人民币,与此同时,相关管理部门推出了针对电商的商品和服务的评价体系现从评价系统中选出200次成功交易,并对其评价进行统计,对商品的好评率为0.6,对服务的好评率为0.75.其中对商品和服务都做出好评的交易为80次.
(1)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.001的前提下,以为商品好评与服务好评有关?
(2)若用分层抽样的方法从“对商品好评”和“商品不满意”中抽出5次交易,再从这5次交易中选出2次,求恰有一次为“商品好评”的概率.
附临界值表:
k2的观测值:$k=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d
关于商品和服务评价的2×2列联表:
(1)先完成关于商品和服务评价的2×2列联表,再判断能否在犯错误的概率不超过0.001的前提下,以为商品好评与服务好评有关?
(2)若用分层抽样的方法从“对商品好评”和“商品不满意”中抽出5次交易,再从这5次交易中选出2次,求恰有一次为“商品好评”的概率.
附临界值表:
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.897 | 10.828 |
关于商品和服务评价的2×2列联表:
| 对服务好评 | 对服务不满意 | 合计 | |
| 对商品好评 | a=80 | b=40 | 120 |
| 对商品不满意 | c=70 | d=10 | 80 |
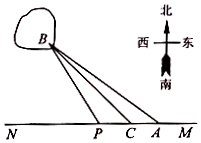 如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.
如图,已知A,B两镇分别位于东西湖岸MN的A处和湖中小岛的B处,点C在A的正西方向1km处,tan∠BAN=$\frac{3}{4}$,∠BCN=$\frac{π}{4}$,现计划铺设一条电缆联通A,B两镇,有两种铺设方案:①沿线段AB在水下铺设;②在湖岸MN上选一点P,先沿线段AP在地下铺设,再沿线段PB在水下铺设,预算地下、水下的电缆铺设费用分别为2万元∕km、4万元∕km.