题目内容
8.若O为△ABC所在平面内任一点,且满足($\overrightarrow{OB}$-$\overrightarrow{OC}$)•($\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$)=0,则△ABC的形状为( )| A. | 等腰三角形 | B. | 直角三角形 | C. | 正三角形 | D. | 等腰直角三角形 |
分析 根据平面向量的线性表示与数量积运算,结合题意可得出△ABC是等腰三角形.
解答 解:因为($\overrightarrow{OB}$-$\overrightarrow{OC}$)•($\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$)=0,
即$\overrightarrow{CB}$•($\overrightarrow{AB}$+$\overrightarrow{AC}$)=0;
又因为$\overrightarrow{AB}$-$\overrightarrow{AC}$=$\overrightarrow{CB}$,
所以($\overrightarrow{AB}$-$\overrightarrow{AC}$)•($\overrightarrow{AB}$+$\overrightarrow{AC}$)=0,
即|$\overrightarrow{AB}$|=|$\overrightarrow{AC}$|,
所以△ABC是等腰三角形.
故选:A.
点评 本题考查了平面向量的线性表示与数量积运算问题,是综合性题目.

练习册系列答案
相关题目
19.已知集合A={x|x>-1},则下列选项正确的是( )
| A. | 0⊆A | B. | {0}⊆A | C. | ∅∈A | D. | {0}∈A |
13.已知集合P=(-∞,0]∪(3,+∞),Q={0,1,2,3},则(∁RP)∩Q=( )
| A. | {0,1} | B. | {0,1,2} | C. | {1,2,3} | D. | {x|0≤x<3} |
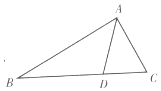 如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.
如图,在△ABC中,$AB=2AC,cosB=\frac{{2\sqrt{5}}}{5}$,点D在线段BC上.