题目内容
函数f（x）=sin（x+
）+asin（x-
）的一条对称轴方程为x=
，则a= ．
| π |
| 3 |
| π |
| 6 |
| π |
| 2 |
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由诱导公式化正弦为余弦，然后化为
sin（x+
-θ），再由x=
时角x+
-θ的终边在y轴上求出θ，则a=tanθ可求．
| a2+1 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
解答：
解：f（x）=sin（x+
）+asin（x-
）
=sin（x+
）-asin（
-x）
=sin（x+
）-acos（x+
）
=
sin（x+
-θ），tanθ=a．
由
+
-θ=kπ+
，得θ=kπ+
，k∈Z．
∴a=tan（kπ+
）=
．
故答案为：
．
| π |
| 3 |
| π |
| 6 |
=sin（x+
| π |
| 3 |
| π |
| 6 |
=sin（x+
| π |
| 3 |
| π |
| 3 |
=
| a2+1 |
| π |
| 3 |
由
| π |
| 2 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
∴a=tan（kπ+
| π |
| 3 |
| 3 |
故答案为：
| 3 |
点评：本题考查y=Asin（ωx+φ）的图象变换，考查了利用两角和与差的正弦化积问题，考查了数学转化思想方法，关键是明确函数的对称轴方程为x=
的意义，是中档题．
| π |
| 2 |
练习册系列答案
相关题目
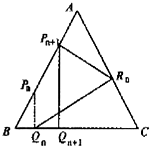已知正△ABC的边长为3，P1是边AB上的一点且BP1=1，从P1向BC作垂线，垂足为Q1，从Q1向CA作垂线，垂足为R1，从R1向AB作垂线，垂足为P2．再从P2重复同样作法，依次得到点Q2，R2，P3，Q3，R3，…Pn，Qn，Rn，…，设BPn=an（n=1，2，3，…）．