题目内容
函数f(x)的定义域为实数集R,f(x)=
对于任意的x∈R都有f(x+1)=f(x-1).若在区间[-1,3]上函数g(x)=f(x)-mx-m恰有四个不同的零点,则实数m的取值范围是 .
|
考点:函数零点的判定定理
专题:函数的性质及应用
分析:先确定2是f(x)的周期,作出函数的图象,利用在区间[-1,3]上函数g(x)=f(x)-mx-m恰有四个不同零点,即可求实数m的取值范围.
解答:
解:由题意,f(x+2)=f[(1+x)+1]=f[(1+x)-1]=f(x),
所以2是f(x)的周期
令h(x)=mx+m,
则函数h(x)恒过点(-1,0),
函数f(x)=
在区间[-1,3]上的图象
如图所示:
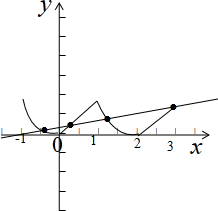
由x=3时,f(3)=1,可得1=3m+m,则m=
∴在区间[-1,3]上函数g(x)=f(x)-mx-m恰有四个不同零点时,实数m的取值范围是(0,
]
故答案为:(0,
].
所以2是f(x)的周期
令h(x)=mx+m,
则函数h(x)恒过点(-1,0),
函数f(x)=
|
如图所示:

由x=3时,f(3)=1,可得1=3m+m,则m=
| 1 |
| 4 |
∴在区间[-1,3]上函数g(x)=f(x)-mx-m恰有四个不同零点时,实数m的取值范围是(0,
| 1 |
| 4 |
故答案为:(0,
| 1 |
| 4 |
点评:本题考查函数的零点,考查数形结合的数学思想,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目

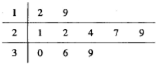 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )