题目内容
以正方形的四个顶点分别作为椭圆的两个焦点和短轴的两个端点,A、B、M是该椭圆上的任意三点(异于椭圆顶点).若存在锐角θ,使
=cosθ•
+sinθ•
,则直线OA、OB的斜率乘积为 .
| OM |
| OA |
| OB |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:首先,可以设椭圆方程为
+
=1,A(x1,y1),B(x2,y2),从而得到
的坐标表示,然后,再根据M点在该椭圆上,建立关系式,结合A、B点在也该椭圆上,得到
+
=1,
+
=1,从而得到相应的结果.
| x2 |
| 2b2 |
| y2 |
| b2 |
| OM |
| ||
| 2b2 |
| ||
| b2 |
| ||
| 2b2 |
| ||
| b2 |
解答:
解:由题意可设椭圆方程为
+
=1,
又设A(x1,y1),B(x2,y2),
=cosθ•
+sinθ•
⇒M(cosθ•x1+sinθ•x2,cosθ•y1+sinθ•y2)
因为M点在该椭圆上,
∴
+
=1,则
又因为A、B点在也该椭圆上,
∴
+
=1,
+
=1
∴
+
=0⇒
=-
,
即直线OA、OB的斜率乘积为-
,
同理当椭圆方程为
+
=1时直线OA、OB的斜率乘积为-2.
故答案为:-
或-2.
| x2 |
| 2b2 |
| y2 |
| b2 |
又设A(x1,y1),B(x2,y2),
| OM |
| OA |
| OB |
因为M点在该椭圆上,
∴
| (cosθ•x1+sinθ•x2)2 |
| 2b2 |
| (cosθ•y1+sinθ•y2)2 |
| b2 |
|
又因为A、B点在也该椭圆上,
∴
| ||
| 2b2 |
| ||
| b2 |
| ||
| 2b2 |
| ||
| b2 |
∴
| 2sinθcosθ•x1x2 |
| 2b2 |
| 2sinθcosθ•y1y2 |
| b2 |
| y1y2 |
| x1x2 |
| 1 |
| 2 |
即直线OA、OB的斜率乘积为-
| 1 |
| 2 |
同理当椭圆方程为
| y2 |
| 2b2 |
| x2 |
| b2 |
故答案为:-
| 1 |
| 2 |
点评:本题重点考查了平面向量的坐标运算,注意审题仔细,本题的表述应说清楚O是坐标原点,且要交待椭圆的位置是以x轴、y轴为对称轴,属于中档题.

练习册系列答案
相关题目
i是虚数单位,复数
-(1-i)2=( )
| 4+2i |
| 1-2i |
| A、0 | B、2 | C、-4i | D、4i |
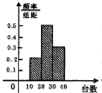
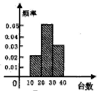
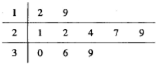 某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )
某公司10个销售店某月销售某产品数量(单位:台)的茎叶图如图,分成[11,20),[20,30),[30,39)时,所作的频率分布直方图是( )