Question

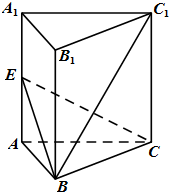如图，正三棱柱ABC-A₁B₁C₁中，AA₁=AB，E是侧棱AA₁的中点．
（Ⅰ）证明：BC₁⊥EC；
（Ⅱ）求二面角A-EC-B的余弦值．

Answer 1

考点：二面角的平面角及求法,空间中直线与直线之间的位置关系

专题：空间位置关系与距离,空间角

分析：（Ⅰ）以AC的中点O为原点，建立空间直角坐标系O-xyz，利用向量法能证明BC₁⊥EC．
（Ⅱ）求出平面AEC的法向量和平面ECD的法向量，利用向量法能示出二面角A-EC-B的余弦值．

解答： （Ⅰ）证明：在正三棱柱中，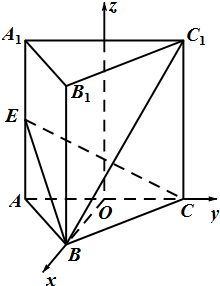
以AC的中点O为原点，建立空间直角坐标系O-xyz如图．
不妨设AB=2，则B

3 ，0，0

，
C

0，1，0

，C1

0，1，2

，E

0，-1，1

，
∴

BC1

=

- 3 ，1，2

，

EC

=

0，2，-1

，
∵

BC1

•

EC

=0+2-2=0．
∴BC₁⊥EC．…（5分）
（Ⅱ）解：在空间直角坐标系O-xyz中，
由题意知平面AEC的一个法向量为

n1

=

1，0，0

．
设平面ECD的法向量为

n2

=

x，y，z

，
易知

BC

=

- 3

，1，0)，

EC

=

0，2，-1

．
由

n2 ⊥ BC n2 ⊥ EC

，得

- 3 x+y=0 2y-z=0

，
取x=1得

n2

=

1， 3 ，2 3

．
cos＜

n1

，

n2

＞=

1

1×4

=

1

4

，
∴二面角A-EC-B的余弦值是

1

4

．

点评：本题考查异面直线垂直的证明，考查二面角的余弦值的求法，解题时要认真审题，注意向量法的合理运用．