题目内容
已知数列{an}是公比为q的等比数列,a1=1,an+2=
(n∈N*)
(1)求{an}的通项公式;
(2)令bn=nan,求{bn}的前n项和Sn.
| an+1+an |
| 2 |
(1)求{an}的通项公式;
(2)令bn=nan,求{bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由已知条件得a1q2=
,解得q=1或q=-
,由此能求出an=1或an=(-
)n-1.
(2)当an=1时,bn=n,Sn=1+2+…+n=
.当an=(-
)n-1时,bn=nan=n•(-
)n-1,由此利用裂项求和法能求出Sn=
-(
+
)•(-
)n.
| a1q+a1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)当an=1时,bn=n,Sn=1+2+…+n=
| n(n+1) |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 9 |
| 4 |
| 9 |
| 2n |
| 3 |
| 1 |
| 2 |
解答:
解:(1)∵数列{an}是公比为q的等比数列,a1=1,an+2=
(n∈N*)
∴a3=
,∴a1q2=
,
∴2q2-q-1=0,
解得q=1或q=-
,
∴an=1或an=(-
)n-1.
(2)当an=1时,bn=n,Sn=1+2+…+n=
.
当an=(-
)n-1时,bn=nan=n•(-
)n-1,
∴Sn=(-
)0+2•(-
)+3•(-
)2+…+n•(-
)n-1,①
-
Sn=(-
)+2•(-
)2+3•(-
)3+…+n•(-
)n,②
①-②,得
Sn=(-
)0+(-
)+(-
)2+…+(-
)n-n•(-
)n
=
-n•(-
)n,
∴Sn=
-(
+
)•(-
)n.
| an+1+an |
| 2 |
∴a3=
| a2+a1 |
| 2 |
| a1q+a1 |
| 2 |
∴2q2-q-1=0,
解得q=1或q=-
| 1 |
| 2 |
∴an=1或an=(-
| 1 |
| 2 |
(2)当an=1时,bn=n,Sn=1+2+…+n=
| n(n+1) |
| 2 |
当an=(-
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=(-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②,得
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
1-(-
| ||
1-(-
|
| 1 |
| 2 |
∴Sn=
| 4 |
| 9 |
| 4 |
| 9 |
| 2n |
| 3 |
| 1 |
| 2 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,解题时要认真审题,注意错位相减法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列式子正确的是( )
A、a2+
| ||||||
B、sinx+
| ||||||
C、
| ||||||
D、x+
|
 小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值.
小华参加学校创意社团,上交一份如图所示的作品:边长为2的正方形中作一内切圆⊙O,在⊙O内作一个关于正方形对角线对称的内接“十”字形图案.OA垂直于该“十”字形图案的一条边,点P为该边上的一个端点.记“十”字形图案面积为S,∠AOP=θ.试用θ表示S,并由此求出S的最大值. 阅读如图所示算法:
阅读如图所示算法: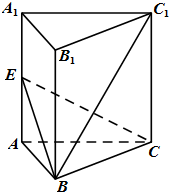 如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.
如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.