题目内容
已知数列{an}的前n项和为Sn,对一切正整数n,点Pn(n,Sn)都在函数f(x)=x2+2x的图象上.
(1)求a1,a2;并求数列{an}的通项公式;
(2)若bn=
=k(
-
),求k,
(3)证明数列{bn}的前n项和Tn<
.
(1)求a1,a2;并求数列{an}的通项公式;
(2)若bn=
| 1 |
| anan+1an+2 |
| 1 |
| anan+1 |
| 1 |
| an+1an+2 |
(3)证明数列{bn}的前n项和Tn<
| 1 |
| 60 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)由已知条件得Sn=n2+2n,n∈N*,由此推导出a1=S1=3,a2=5,an=Sn-Sn-1=2n+1,由此能求出数列{an}的通项公式.
(2)由(1)得bn=
=
[
-
],由此能求出k.
(3)利用裂项求和法求出Tn=
[
-
]=
-
,由此能证明Tn<
.
(2)由(1)得bn=
| 1 |
| (2n+1)(2n+3)(2n+5) |
| 1 |
| 4 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| (2n+3)(2n+5) |
(3)利用裂项求和法求出Tn=
| 1 |
| 4 |
| 1 |
| 3×5 |
| 1 |
| (2n+3)(2n+5) |
| 1 |
| 60 |
| 1 |
| 4(2n+3)(2n+5) |
| 1 |
| 60 |
解答:
(1)解:∵点Pn(n,Sn)都在函数f(x)=x2+2x的图象上.
∴Sn=n2+2n,n∈N*,
∴a1=S1=3,(2分)
又a1+a2=S2=22+2×2=8,∴a2=5.(4分)
由(1)知,Sn=n2+2n,n∈N*,
当n≥2时,an=Sn-Sn-1=2n+1,(6分)
由(1)知,a1=3=2×1+1满足上式,(7分)
∴数列{an}的通项公式为an=2n+1.(8分)
(2)解:由(1)得bn=
=
[
-
],
∵bn=
=k(
-
),
∴k=
.
(3)证明:Tn=
[
-
+
-
+…+
-
](12分)
=
[
-
]
=
-
<
.
∴Tn<
.(14分)
∴Sn=n2+2n,n∈N*,
∴a1=S1=3,(2分)
又a1+a2=S2=22+2×2=8,∴a2=5.(4分)
由(1)知,Sn=n2+2n,n∈N*,
当n≥2时,an=Sn-Sn-1=2n+1,(6分)
由(1)知,a1=3=2×1+1满足上式,(7分)
∴数列{an}的通项公式为an=2n+1.(8分)
(2)解:由(1)得bn=
| 1 |
| (2n+1)(2n+3)(2n+5) |
=
| 1 |
| 4 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| (2n+3)(2n+5) |
∵bn=
| 1 |
| anan+1an+2 |
| 1 |
| anan+1 |
| 1 |
| an+1an+2 |
∴k=
| 1 |
| 4 |
(3)证明:Tn=
| 1 |
| 4 |
| 1 |
| 3×5 |
| 1 |
| 5×7 |
| 1 |
| 5×7 |
| 1 |
| 7×9 |
| 1 |
| (2n+1)(2n+3) |
| 1 |
| (2n+3)(2n+5) |
=
| 1 |
| 4 |
| 1 |
| 3×5 |
| 1 |
| (2n+3)(2n+5) |
=
| 1 |
| 60 |
| 1 |
| 4(2n+3)(2n+5) |
| 1 |
| 60 |
∴Tn<
| 1 |
| 60 |
点评:本题考查数列的通项公式的求法,考查不等式的证明,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
当x=5时.用秦九韶算法计算f(x)=12x6+5x5+11x2+2x+5的值时,需要进行的乘法和加法的次数分别是( )
| A、12,6 | B、6,6 |
| C、15,4 | D、6,4 |
设实数a,b,c满足a+b+c=0,则a,b,c中( )
| A、至多有一个不大于0 |
| B、至少有一个不小于0 |
| C、至多有两个不小于0 |
| D、至少有两个不小于0 |
下列式子正确的是( )
A、a2+
| ||||||
B、sinx+
| ||||||
C、
| ||||||
D、x+
|
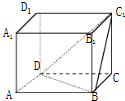 如图长方体ABCD-A1B1C1D1中,AB=AD=2
如图长方体ABCD-A1B1C1D1中,AB=AD=2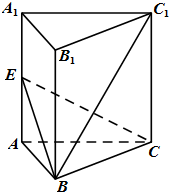 如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.
如图,正三棱柱ABC-A1B1C1中,AA1=AB,E是侧棱AA1的中点.