题目内容
已知椭圆
+
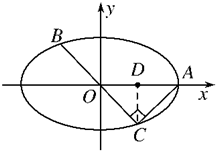
=1(a>b>0),A(6,0)为长轴的一个端点,弦BC过椭圆的中心O,
•
=0且|
-
|=2|
|,则椭圆的焦距是( )
| x2 |
| a2 |
| y2 |
| b2 |
| AC |
| BC |
| OB |
| OC |
| AC |
A、2
| ||
B、2
| ||
C、4
| ||
D、4
|
考点:椭圆的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意可知且a=6,进而可确定C(3,-3),代入椭圆方程,从而可求椭圆的焦距.
解答:
 解:∵
解:∵
•
=0且|
-
|=2|
|,
∴|BC|=2|AC|,AC⊥BC,
由椭圆的结构特征可得:|OC|=|AC|,
∵A(6,0)为长轴的一个端点,即a=6,
∴C点的横坐标为3,即C(3,-3),
∵点C在椭圆
+
=1(a>b>0)上,
∴b2=12,∴c2=24
∴c=2
,
∴2c=4
.
故选:C.
 解:∵
解:∵| AC |
| BC |
| OB |
| OC |
| AC |
∴|BC|=2|AC|,AC⊥BC,
由椭圆的结构特征可得:|OC|=|AC|,
∵A(6,0)为长轴的一个端点,即a=6,
∴C点的横坐标为3,即C(3,-3),
∵点C在椭圆
| x2 |
| a2 |
| y2 |
| b2 |
∴b2=12,∴c2=24
∴c=2
| 6 |
∴2c=4
| 6 |
故选:C.
点评:本题重点考查椭圆的性质,考查向量知识的运用,解题的关键是求出点C的坐标,从而可求出椭圆的方程.

练习册系列答案
相关题目
在△ABC中,角A、B、C所对的边分别为a、b、c,若A:B:C=3:2:1,则a:b:c=( )
| A、3:2:1 | ||||
B、
| ||||
C、
| ||||
D、2:
|
设等差数列{an}的前n项和为Sn,已知S2+S6=0,a4=1,则a5=( )
| A、-2 | B、-1 | C、0 | D、2 |
设集合A={x|x2-3x+2>0,x∈R},集合B为函数y=lg(3-x)的定义域,则A∩B=( )
| A、(0,1)∪(2,3) |
| B、(-∞,1)∪(2,3) |
| C、(-∞,1)∪(2,+∞) |
| D、(3,+∞) |
在数列{an}中,a1=4,a2=10,若{log3(an-1)}为等差数列,且Tn=
+
+…+
等于( )
| 1 |
| a2-a1 |
| 1 |
| a3-a2 |
| 1 |
| an+1-an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在数列{an}中,已知a1=2,an=an-1+n(n≥2,n∈N*),则a4等于( )
| A、4 | B、11 | C、10 | D、8 |
要得到函数y=cos(2x+
)的图象,可以将函数y=cos2x的图象( )
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
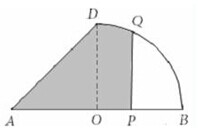 如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )
如图,△ABD是一直角边为1的直角等腰三角形,平面图形OBD是四分之一圆的扇形,点P在线段AB上,PQ⊥AB,且PQ交AD或交弧DB于点Q,设AP=x(0<x<2),图中阴影部分这平面图形APQ(或APQD)的面积为y,则函数y=f(x)的大致图象是( )


