题目内容
18.已知直线l的参数方程为$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4$\sqrt{2}$sin(θ-$\frac{π}{4}$).(1)求圆C的直角坐标方程;
(2)若点M(x,y)是直线l与圆面ρ≤4$\sqrt{2}$sin(θ-$\frac{π}{4}$)的公共点,求$\sqrt{2}$x+$\sqrt{2}$y的取值范围.
分析 (1)圆C的极坐标方程为ρ=4$\sqrt{2}$sin(θ-$\frac{π}{4}$),ρ2=ρ•4$\sqrt{2}$sin(θ-$\frac{π}{4}$).展开ρ2=ρ•4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$(sinθ-cosθ).利用互化公式即可得出直角坐标方程.
(2)由x2+y2=4x-4y配方可得:(x-2)2+(y+2)2=8.设M坐标:$\left\{\begin{array}{l}{x=2+2\sqrt{2}rcosθ}\\{y=-2+2\sqrt{2}rsinθ}\end{array}\right.$,$(0≤r≤2\sqrt{2})$.再利用和差公式及其单调性值域即可得出.
解答 解:(1)圆C的极坐标方程为ρ=4$\sqrt{2}$sin(θ-$\frac{π}{4}$),ρ2=ρ•4$\sqrt{2}$sin(θ-$\frac{π}{4}$).
∴ρ2=ρ•4$\sqrt{2}$×$\frac{\sqrt{2}}{2}$(sinθ-cosθ).
∴x2+y2=4x-4y.
(2)由x2+y2=4x-4y配方可得:(x-2)2+(y+2)2=8.
设M坐标:$\left\{\begin{array}{l}{x=2+2\sqrt{2}rcosθ}\\{y=-2+2\sqrt{2}rsinθ}\end{array}\right.$,$(0≤r≤2\sqrt{2})$.
∴$\sqrt{2}$x+$\sqrt{2}$y=$\sqrt{2}$$(2+2\sqrt{2}rcosθ)$+$\sqrt{2}$$(2+2\sqrt{2}rsinθ)$
=4$\sqrt{2}$+4$\sqrt{2}$rsin$(θ+\frac{π}{4})$∈$[0,8\sqrt{2}]$.
点评 本题考查了极坐标方程回去直角坐标方程、三角函数的单调性与值域、和差公式,考查了推理能力与计算能力,属于中档题.

 天天练口算系列答案
天天练口算系列答案| A. | 1 | B. | -1 | C. | i | D. | -i |
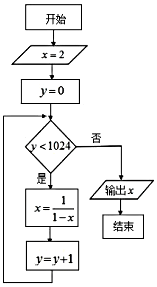
| A. | 2016 | B. | 1024 | C. | $\frac{1}{2}$ | D. | -1 |
| A. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B. | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C. | $\lim_{n→∞}{a_n}$存在,$\lim_{n→∞}{S_n}$不存在 | D. | $\lim_{n→∞}{a_n}$不存在,$\lim_{n→∞}{S_n}$存在 |