已知(2-i)=4+3i.则z的虚部为( )A．1B．-1C．iD．-i 题目和参考答案——青夏教育精英家教网—

题目内容

9．已知（$\overline{z}$-1+3i）（2-i）=4+3i（其中i是虚数单位），则z的虚部为（　　）

A．

B．

-1

C．

D．

-i

分析利用复数的运算法则、共轭复数的定义、虚部的定义即可得出．

解答解：∵（$\overline{z}$-1+3i）（2-i）=4+3i，
∴$\overline{z}$-1+3i=$\frac{4+3i}{2-i}$=$\frac{（4+3i）（2+i）}{（2-i）（2+i）}$=1+2i，
∴$\overrightarrow{z}$=2-i，
∴z=2+i，
∴z的虚部为1，
故选：A．

点评本题考查了复数的运算法则、共轭复数的定义、虚部的定义，考查了推理能力与计算能力，属于中档题．

练习册系列答案

相关题目

设函数

（1）求的定义域；

（2）时，求使的所有值．

20．已知一种腌菜食品按行业生产标准分为A，B，C三个等级，现针对某加工厂同一批次的三个等级420箱腌菜进行质量检测，采用分层抽样的方法进行抽取．设从三个等级A，B，C中抽取的箱数分别为m，n，t，若2t=m+n，则420箱腌菜中等级为C级的箱数为（　　）

17．已知函数f（x）=xlnx，g（x）=$\frac{a}{2}{x^2}$+x-a（a∈R）．
（Ⅰ）若直线x=m（m＞0）与曲线y=f（x）和y=g（x）分别交于M，N两点．设曲线y=f（x）在点M处的切线为l₁，y=g（x）在点N处的切线为l₂．
（ⅰ）当m=e时，若l₁⊥l₂，求a的值；
（ⅱ）若l₁∥l₂，求a的最大值；
（Ⅱ）设函数h（x）=f（x）-g（x）在其定义域内恰有两个不同的极值点x₁，x₂，且x₁＜x₂．若λ＞0，且λlnx₂-λ＞1-lnx₁恒成立，求λ的取值范围．

4．

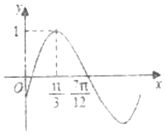函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，$|φ|＜\frac{π}{2}$）的图象如图所示，为了得到g（x）=Asinωx的图象，可以将f（x）的图象（　　）

	A．	向左平移$\frac{π}{12}$个单位长度		B．	向右平移$\frac{π}{12}$个单位长度
	C．	向左平移$\frac{π}{6}$个单位长度		D．	向右平移$\frac{π}{6}$个单位长度

14．设$a={log_5}4，b={log_{\sqrt{2}}}3，c={（{{{log}_{0.2}}3}）^2}$，则a，b，c的大小关系为（　　）

1．已知向量$\overrightarrow a=（{1，1}），\overrightarrow b=（{-1，0}）$，若向量$k\overrightarrow a+\overrightarrow b$与向量$\overrightarrow c=（{2，1}）$共线，则实数k=-1．

18．已知直线l的参数方程为$\left\{\begin{array}{l}{x=-2+\frac{\sqrt{2}}{2}t}\\{y=2+\frac{\sqrt{2}}{2}t}\end{array}\right.$（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为ρ=4$\sqrt{2}$sin（θ-$\frac{π}{4}$）．
（1）求圆C的直角坐标方程；
（2）若点M（x，y）是直线l与圆面ρ≤4$\sqrt{2}$sin（θ-$\frac{π}{4}$）的公共点，求$\sqrt{2}$x+$\sqrt{2}$y的取值范围．

19．将函数$y=sin（{\frac{π}{6}-2x}）$的图象向右平移$\frac{π}{12}$个单位后得到的图象的一个对称轴是（　　）