题目内容
7．已知数列{an}满足：an=$\left\{\begin{array}{l}{1，1≤n≤2016}\\{2•（\frac{1}{3}）^{n-2016}，n≥2017}\end{array}\right.$，设Sn表示数列{an}的前n项和．则下列结论正确的是（ ）| A． | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都存在 | B． | $\lim_{n→∞}{a_n}$和$\lim_{n→∞}{S_n}$都不存在 | ||
| C． | $\lim_{n→∞}{a_n}$存在，$\lim_{n→∞}{S_n}$不存在 | D． | $\lim_{n→∞}{a_n}$不存在，$\lim_{n→∞}{S_n}$存在 |
分析 推导出Sn=2017-（$\frac{1}{3}$）n-2016，根据极限的定义即可判断．
解答 解：∵数列{an}，对任意的正整数n，an=$\left\{\begin{array}{l}{1，1≤n≤2016}\\{2•（\frac{1}{3}）^{n-2016}，n≥2017}\end{array}\right.$，设Sn表示数列{an}的前n项和，
∴a1=a2=a3=…=a2016=1，a2017=-$\frac{2}{3}$，a2018=-$\frac{2}{9}$，a2019=-$\frac{2}{27}$，…，
∴Sn=2016+$\frac{\frac{2}{3}[1-（\frac{1}{3}）^{n-2016}]}{1-\frac{1}{3}}$=2016+1-（$\frac{1}{3}$）n-2016=2017-（$\frac{1}{3}$）n-2016，
$\lim_{n→∞}{S_n}$=$\underset{lim}{n→∞}$[2017-（$\frac{1}{3}$）n-2016]=2017，$\lim_{n→∞}{a_n}$=$\underset{lim}{n→∞}$（2×（$\frac{1}{3}$）n-2016）=0，
故选：A
点评 本题考查了分组求和和极限的定义，属于中档题．
练习册系列答案
相关题目
15．若α是第四象限角，且$cosα=\frac{3}{5}$，则tan2α=（ ）
| A． | $-\frac{4}{3}$ | B． | $-\frac{24}{7}$ | C． | $\frac{24}{7}$ | D． | $\frac{24}{25}$ |
19．将函数$y=sin（{\frac{π}{6}-2x}）$的图象向右平移$\frac{π}{12}$个单位后得到的图象的一个对称轴是（ ）
| A． | $x=\frac{π}{6}$ | B． | $x=\frac{π}{3}$ | C． | $x=\frac{5π}{12}$ | D． | $x=\frac{π}{3}$ |
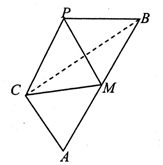已知△ABC中，∠C=90°，tanA=$\sqrt{2}$，M为AB的中点，现将△ACM沿CM折成三棱锥P-CBM，当二面角P-CM-B大小为60°时，$\frac{AB}{PB}$=$\sqrt{3}$．