题目内容
8.已知函数f(x)对任意的实数x均满足f(x)=-f(2-x),且在[1,+∞)上递增,g(x)=f(1+x),且2g(log2a)-3g(1)≤g(log${\;}_{\frac{1}{2}}$a),则实数a的取值范围为(0,2].分析 先判断函数f(x)的对称性,再判断g(x)的奇偶性和单调区间,化简不等式解得即可.
解答 解:∵函数f(x)对?x∈R满足f(x)=-f(2-x),∴f(x)的图象关于点(1,0)对称.
∵g(x)=f(1+x),f(x)在[1,+∞)上递增,
∴g(x)为奇函数,并且在[0,+∞)是增函数.
∵2g(log2a)-3g(1)≤g(log${\;}_{\frac{1}{2}}$a)=g(-log2a)=-g(log2a),
∴3g(log2a)≤3g(1)
即log2a≤1=log22,∴0<a≤2,
故答案为:(0,2].
点评 本题考查了函数的奇偶性和单调性的综合应用,注意自变量的取值范围,考查了学生的转化能力,属于中档题.

练习册系列答案
 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
2.若存在实数x,使|x-a|+|x-1|≤3成立,则实数a的取值范围是( )
| A. | [-2,1] | B. | [-2,2] | C. | [-2,3] | D. | [-2,4] |

 的定义域;
的定义域; 时,求使
时,求使 的所有
的所有 值.
值.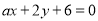 与l2:
与l2: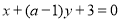 平行,那么a等于( )
平行,那么a等于( )