题目内容
在△ABC中,过点A做∠BAC的平分线交BC于D,证明:AB:BD=AC:CD (用正弦定理证)
考点:正弦定理
专题:证明题,解三角形
分析:在△ABD中,由正弦定理得
=
=
,在△ACD中,由正弦定理得
=
=
,由sinD1=sinD2,sinA1=sinA2,即可得证.
| AD |
| sinB |
| AB |
| sinD1 |
| BD |
| sinA1 |
| AD |
| sinC |
| AC |
| sinD2 |
| DC |
| sinA2 |
解答:
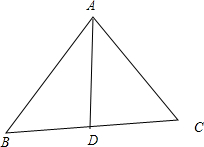 解:在△ABD中,由正弦定理可得:
解:在△ABD中,由正弦定理可得:
=
=
;
在△ACD中,由正弦定理可得:
=
=
;
因为:sinD1=sinD2,sinA1=sinA2,
可得:
=
=
=
,
即有:AB:BD=AC:CD,从而得证.
 解:在△ABD中,由正弦定理可得:
解:在△ABD中,由正弦定理可得:| AD |
| sinB |
| AB |
| sinD1 |
| BD |
| sinA1 |
在△ACD中,由正弦定理可得:
| AD |
| sinC |
| AC |
| sinD2 |
| DC |
| sinA2 |
因为:sinD1=sinD2,sinA1=sinA2,
可得:
| AB |
| BD |
| sinD1 |
| sinA1 |
| sinD2 |
| sinA2 |
| AC |
| DC |
即有:AB:BD=AC:CD,从而得证.
点评:本题主要考查了正弦定理的应用,考查了角平分线的性质,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在数列{an}中,an>0,a1=
,如果an+1是1与
的等比中项,那么a1+
+
+
+…+
的值是( )
| 1 |
| 2 |
| 2anan+1+1 |
| 4-an2 |
| a2 |
| 22 |
| a3 |
| 32 |
| a4 |
| 42 |
| a100 |
| 1002 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知F1,F2是椭圆和双曲线的公共焦点,P是它们的一个公共点,且∠F1PF2=
,则椭圆和双曲线的离心率的倒数之和的最大值为( )
| π |
| 3 |
| A、3 | ||||
B、
| ||||
| C、2 | ||||
D、
|
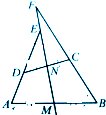 已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证:
已知:如图,M,N是四边形ABCD中AB和CD的中点,AD的延长线、BC的延长线分别交直线MN与点E,F,求证: