题目内容
19.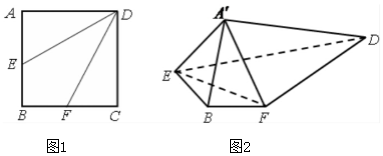 如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.
如图,边长为2的正方形ABCD中,点E是AB的中点,点F是BC的中点.将△AED、△DCF分别沿DE、DF折起,使A、C两点重合于点A',连结EF,A'B.(1)求异面直线A'D与EF所成角的大小;
(2)求三棱锥D-A'EF的体积.
分析 (1)在正方形ABCD中,有AD⊥AE,CD⊥CF,可得A'D⊥A'E,A'D⊥A'F,由线面垂直的判定可得A'D⊥平面A'EF.从而得到A'D⊥EF;
(2)已知正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,可得A'E2+A'F2=EF2,则A'E⊥A'F,求出三角形A′EF的面积,结合(1)可知三棱锥D-A'EF的高A'D=2,代入棱锥体积公式求得三棱锥D-A'EF的体积.
解答 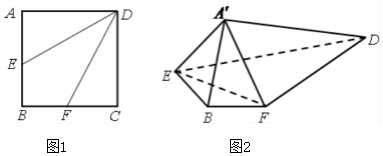 解:(1)在正方形ABCD中,
解:(1)在正方形ABCD中,
∵AD⊥AE,CD⊥CF,∴A'D⊥A'E,A'D⊥A'F,
又A'E∩A'F=A',A'E,A'F?平面A'EF,∴A'D⊥平面A'EF.
而EF?平面A'EF,∴A'D⊥EF,
∴异面直线A'D与EF所成角的大小为90°;
(2)∵正方形ABCD的边长为2,点E是AB的中点,点F是BC的中点,
∴在Rt△BEF中,BE=BF=1,得$EF=\sqrt{2}$,
而A'E=A'F=1,
∴A'E2+A'F2=EF2,则A'E⊥A'F,
∴${S_△}_{A'EF}=\frac{1}{2}×1×1=\frac{1}{2}$,
由(1)得A'D⊥平面A'EF,且A'D=2,
∴${V_{D-A'EF}}=\frac{1}{3}{S_{△A'EF}}A'D=\frac{1}{3}×\frac{1}{2}×2=\frac{1}{3}$.
点评 本题考查平面与平面平行的判定,考查空间想象能力和思维能力,训练了多面体体积的求法,属中档题.

练习册系列答案
相关题目
9.若命题p:?x0>0,|x0|≤1,则命题p的否定是( )
| A. | ?x>0,|x|>1 | B. | ?x>0,|x|≥1 | C. | ?x≤0,|x|<1 | D. | ?x≤0,|x|≤1 |
10.若存在实数α∈R,$β∈[\frac{π}{2},π]$,使得实数t同时满足$t={cos^2}β+\frac{α}{2}cosβ$,α≤t≤α-2cosβ,则t的取值范围是( )
| A. | $[-\frac{2}{3},0]$ | B. | $[0,\frac{4}{3}]$ | C. | $[\frac{4}{3},2]$ | D. | [2,4] |
11.给出定义:设f′(x)是函数y=f(x)的导函数,f″(x)是函数f′(x)的导函数,若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.已知函数f(x)=-4x+3sinx-cosx的拐点是M(x0,f(x0)),则点M( )
| A. | 在直线y=-3x上 | B. | 在直线y=3x上 | C. | 在直线y=-4x上 | D. | 在直线y=4x上 |
8.与x轴相切且和半圆x2+y2=4(0≤y≤2)内切的动圆圆心的轨迹方程是( )
| A. | x2=-4(y-1)(0<y≤1) | B. | x2=4(y-1)(0<y≤1) | C. | x2=4(y+1)(0<y≤1) | D. | x2=-2(y-1)(0<y≤1) |
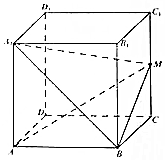 已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.
已知棱长为1的正方体ABCD-A1B1C1D1中,M是棱CC1的中点,则三棱锥A1-ABM的体积为$\frac{1}{6}$.