题目内容
已知集合A=Z,B={x|x=2n+1,n∈Z},C=R,若A到B的映射是f:x→y=2x-1,B到C的映射是g:y→z=
y+1,求A→C的映射h:x→z的对应法则.
| 1 |
| 3 |
考点:映射
专题:函数的性质及应用
分析:由已知中A到B的映射是f:x→y=2x-1,B到C的映射是g:y→z=
y+1,将g中y替换成2x-1后,整理可得A→C的映射h:x→z的对应法则.
| 1 |
| 3 |
解答:
解:∵A到B的映射是f:x→y=2x-1,B到C的映射是g:y→z=
y+1,
∴A→C的映射h:x→z的对应法则z=
(2x-1)+1=
x+
| 1 |
| 3 |
∴A→C的映射h:x→z的对应法则z=
| 1 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
点评:本题考查的知识点是映射,难度不大,属于基础题.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
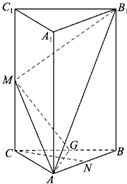 如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=
如图,在正三棱柱ABC-A1B1C1中,底面ABC为正三角形,M、N、G分别是棱CC1、AB、BC的中点.且CC1=