题目内容
二项式(x2-
)11的展开式中,系数最大的项为( )
| 1 |
| x |
| A、第五项 | B、第六项 |
| C、第七项 | D、第六和第七项 |
考点:二项式系数的性质
专题:二项式定理
分析:在二项展开式的通项公式中,根据二项式的展式的通项公式为Tr+1=(-1)r•
•x22-3r,可得系数最大的项.
| C | r 11 |
解答:
解:二项式(x2-
)11的展式的通项公式为 Tr+1=
•x22-2r•(-1)r•x-r =(-1)r•
•x22-3r,
故当r=6时,展开式的系数(-1)r•
=
最大,
故选:C.
| 1 |
| x |
| C | r 11 |
| C | r 11 |
故当r=6时,展开式的系数(-1)r•
| C | r 11 |
| C | 6 11 |
故选:C.
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切,则圆C的方程是( )
| A、(x+1)2+y2=2 |
| B、(x+1)2+y2=8 |
| C、(x-1)2+y2=2 |
| D、(x-1)2+y2=8 |
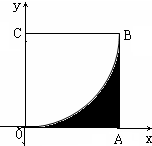 如图,已知正方形OABC的四个顶点坐标分别为O(0,0),A(1,0),B(1,1),C(0,1),现向该正方体内部随机投1000个点,统计出所投点落在阴影部分的个数为328,由此估计图中阴影部分的面积为( )
如图,已知正方形OABC的四个顶点坐标分别为O(0,0),A(1,0),B(1,1),C(0,1),现向该正方体内部随机投1000个点,统计出所投点落在阴影部分的个数为328,由此估计图中阴影部分的面积为( )| A、0.328 | B、0.672 |
| C、0.3 | D、0.7 |
 已知四棱锥P-ABCD的三视图如图所示,则四棱锥的外接球的表面积为( )
已知四棱锥P-ABCD的三视图如图所示,则四棱锥的外接球的表面积为( )| A、24π | ||
| B、6π | ||
C、
| ||
| D、3π |
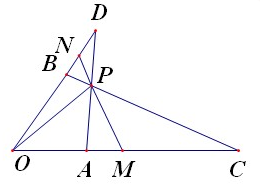 如图,
如图,