题目内容
已知函数f(x)=2|ex-ea|-
+ea,x∈(0,1],a∈R
(1)当a≥1时,求函数f(x)的单调区间;
(2)当a∈(0,1)时,求函数f(x)的最大值的表达式M(a).
| ex |
| x |
(1)当a≥1时,求函数f(x)的单调区间;
(2)当a∈(0,1)时,求函数f(x)的最大值的表达式M(a).
考点:利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)由a≥1和x∈(0,1]可得ex-ea≤0,求得f(x)=3ea-2ex-
,求导后由导函数大于0和导函数小于0求得函数f(x)的单调区间;
(2)由x的范围写出分段函数f(x),由(1)可知x∈(0,a]的单调性,再分析出x∈(a,1]上的单调性,然后分0<a≤
和
<a<1求得函数f(x)的最大值M(a).
| ex |
| x |
(2)由x的范围写出分段函数f(x),由(1)可知x∈(0,a]的单调性,再分析出x∈(a,1]上的单调性,然后分0<a≤
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)当a≥1时,又x∈(0,1],
∴ex-ea≤0恒成立,则f(x)=3ea-2ex-
,
∴f′(x)=-2ex-
=-
(2x2+x-1),
当x>
时,f'(x)<0;
当0<x<
时,f'(x)>0,又x∈(0,1],
∴函数f(x)的单调递增区间为(0,
),单调递减区间为(
,1];
(2)f(x)=
,
当x∈(a,1],f(x)=2ex-
-ea,
f′(x)=
(2x2-x+1)=
×[2(x-
)2+
]>0,
∴x∈(a,1]时,f(x)=2ex-
-ea单调递增.
(i)当0<a≤
时,f(x)在(0,a]单调递增,在[a,1]上单调递增,
则M(a)=f(x)max=f(1)=e-ea;
(ii)当
<a<1时,f(x)在(0,
]单调递增,在(
,a)单调递减,在[a,1]上单调递增,
函数f(x)的最大值在f(1)与f(
)中取到,
∵f(1)=e-ea,f(
)=3ea-4
,
由f(
)>f(1),即3ea-4
>e-ea,得a>ln
,
∴当ln
<a<1时,f(
)>f(1),M(a)=f(x)max=f(
)=3ea-4
;
当
<a≤ln
时,f(
)≤f(1),M(a)=f(x)max=f(1)=e-ea.
综上,M(a)=
.
∴ex-ea≤0恒成立,则f(x)=3ea-2ex-
| ex |
| x |
∴f′(x)=-2ex-
| ex(x-1) |
| x2 |
| ex |
| x2 |
当x>
| 1 |
| 2 |
当0<x<
| 1 |
| 2 |
∴函数f(x)的单调递增区间为(0,
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(x)=
|
当x∈(a,1],f(x)=2ex-
| ex |
| x |
f′(x)=
| ex |
| x2 |
| ex |
| x2 |
| 1 |
| 4 |
| 7 |
| 8 |
∴x∈(a,1]时,f(x)=2ex-
| ex |
| x |
(i)当0<a≤
| 1 |
| 2 |
则M(a)=f(x)max=f(1)=e-ea;
(ii)当
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
函数f(x)的最大值在f(1)与f(
| 1 |
| 2 |
∵f(1)=e-ea,f(
| 1 |
| 2 |
| e |
由f(
| 1 |
| 2 |
| e |
4
| ||
| 4 |
∴当ln
4
| ||
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| e |
当
| 1 |
| 2 |
4
| ||
| 4 |
| 1 |
| 2 |
综上,M(a)=
|
点评:本题考查了利用导数研究函数的单调性,考查了利用导数求函数的最值,正确分类是解答该题的关键,考查了学生综合分析问题和解决问题的能力,是压轴题.

练习册系列答案
相关题目
方程log
x=2x-2014的实数根的个数为( )
| 1 |
| 2 |
| A、0 | B、1 | C、2 | D、不确定 |
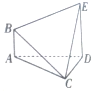 在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.
在如图所示的多面体ABEDC中,AB⊥平面ACD,DE⊥平面ACD,DE⊥平面ACD,且AC=CD,DE=2AB=2,AD=2,∠ACD=90°.求多面体ABEDC的体积.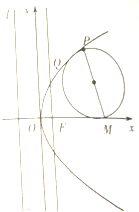 如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一点,Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为
如图,设F为抛物线y2=2px(p>0)的焦点,P是抛物线上一点,Q为线段OF的垂直平分线上一点,且点Q到抛物线的准线l的距离为