题目内容
过抛物线y2=ax 的焦点作直线交抛物线于A(x1,y1),B(x2,y2)两点,如果x1+x2=8且|AB|=10,则a= .
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:由题意可得a>0,然后直接由抛物线的焦点弦长公式结合已知求得a的值.
解答:
解:由抛物线方程y2=ax,且抛物线上两点A(x1,y1),B(x2,y2)满足x1+x2=8,
可知a>0,即2p=a>0,∴p=
>0.
由抛物线的焦点弦公式得:|AB|=x1+x2+p,
∵x1+x2=8且|AB|=10,
∴10=8+p,即p=2,
∴
=2,a=4.
故答案为:4.
可知a>0,即2p=a>0,∴p=
| a |
| 2 |
由抛物线的焦点弦公式得:|AB|=x1+x2+p,
∵x1+x2=8且|AB|=10,
∴10=8+p,即p=2,
∴
| a |
| 2 |
故答案为:4.
点评:本题考查了抛物线的简单几何性质,考查了抛物线的焦点弦长公式,是基础题.

练习册系列答案
相关题目
数列中{an}中,an+1=
,a1=1,则a5=( )
| 2an |
| 2+an |
A、
| ||
B、
| ||
C、
| ||
D、
|
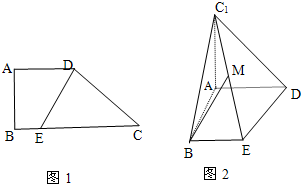 如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=
如图1,直角梯形ABCD中,AD∥BC,∠ABC=90°,AD=AB=