Question

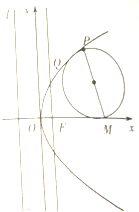如图，设F为抛物线y²=2px（p＞0）的焦点，P是抛物线上一点，Q为线段OF的垂直平分线上一点，且点Q到抛物线的准线l的距离为

3

2

．
（1）求抛物线的方程；
（2）设点M的坐标为（3，0），是否垂直于x轴的直线l′被以PM为直径的圆截得的弦长为定值？若存在，求直线l′的方程；若不存在，请说明理由．

Answer 1

考点：抛物线的简单性质

专题：圆锥曲线的定义、性质与方程

分析：（1）由抛物线方程求出焦点坐标，进一步得到Q的横坐标，由

p

4

-(-

p

2

)=

3p

4

=

3

2

求得p的值，则抛物线方程可求；
（2）设MP的中点为S，垂直于x轴的直线方程为x=a，以MP为直径的圆交l于A，B两点，AB的中点为H，然后由圆当中的半径、弦心距间的关系列式得到垂直于x轴的直线l′被以PM为直径的圆截得的半弦长的平方等于（a-2）x-a²+3a，当a=2时所得值与x无关，为定值．

解答： 解：（1）由y²=2px（p＞0），得F（

p

2

，0），
∵Q为线段OF的垂直平分线上一点，
∴xQ=

p

4

，
由点Q到抛物线的准线l的距离为

3

2

，得

p

4

-(-

p

2

)=

3p

4

=

3

2

，
∴p=2．
则抛物线的方程为y²=4x；
（2）设MP的中点为S，垂直于x轴的直线方程为x=a，
以MP为直径的圆交l于A，B两点，AB的中点为H，
∵|AS|=

1

2

|MP|=

(x-3)2+y2

，
|SH|=|

x+3

2

-a|=

1

2

|x-2a+3|，
∴|AH|²=|AS|²-|SH|²=

1

4

[(x-3)2+y2]-

1

4

(x-2a+3)2
=

1

4

[(4a-8)x-4a2+12a]=（a-2）x-a²+3a，
令a=2，则对任意满足条件的x，
都有|AH|²=-4+6=2（与x无关），
即|AB|=2

2

为定值．

点评：本题考查了抛物线方程的求法，考查了直线与抛物线的关系，体现了数学转化思想方法，是中档题．