题目内容
3.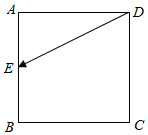 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
分析 建系,由向量数量积的坐标运算公式,分类讨论,结合点E的运动,即可求出最大值.
解答 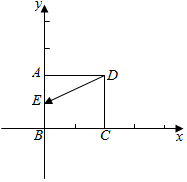 解:以BC、BA所在直线为x轴、y轴,建立坐标系如图
解:以BC、BA所在直线为x轴、y轴,建立坐标系如图
可得A(0,1),B(0,0),C(1,0),D(1,1),
当E在DA上,设E(x,1),其中0≤x≤1
∵$\overrightarrow{DE}$=(x-1,0),$\overrightarrow{CD}$=(0,1),
∴$\overrightarrow{DE}•\overrightarrow{CD}$=0,
当E在AB上,设E(0,y),其中0≤y≤1
∵$\overrightarrow{DE}$=(-1,y-1),$\overrightarrow{CD}$=(0,1),
∴$\overrightarrow{DE}•\overrightarrow{CD}$=y-1,(0≤y≤1),此时最大值为0,
当E在BC上,设E(x,0),其中0≤x≤1
∵$\overrightarrow{DE}$=(x-1,-1),$\overrightarrow{CD}$=(0,1),
∴$\overrightarrow{DE}•\overrightarrow{CD}$=-1,
当E在CD上,设E(1,y),其中0≤y≤1
∵$\overrightarrow{DE}$=(0,y-1),$\overrightarrow{CD}$=(0,1),
∴$\overrightarrow{DE}•\overrightarrow{CD}$=y-1,(0≤y≤1),此时最大值为0,
综上所述$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是0,
故选:A.
点评 本题考查向量数量积的最大值,建立坐标系是解决问题的关键,属中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知集合A={x|y=$\sqrt{2-x}}$},B={x|x2-2x<0},则( )
| A. | A∩B=∅ | B. | A∪B=R | C. | B⊆A | D. | A⊆B |
 为圆
为圆 的弦
的弦 的中点,则直线
的中点,则直线 的方程是( )
的方程是( ) B.
B.
 D.
D.