题目内容

8．已知集合A={x|y=$\sqrt{2-x}}$}，B={x|x2-2x＜0}，则（　　）
A．A∩B=∅B．A∪B=RC．B⊆AD．A⊆B

分析 求出集合A，B，根据集合包含关系的定义，可得答案．

解答 解：∵集合A={x|y=$\sqrt{2-x}}$}=（-∞，2]，B={x|x2-2x＜0}=（0，2），
故B⊆A，
故选：C．

点评 本题考查的知识点是集合的包含关系判断及应用，函数的定义域，二次不等式的解法，难度中档．

练习册系列答案
相关题目
1．已知函数f0（x）=x（sinx+cosx），设fn（x）是fn-1（x）的导数，n∈N*．
（1）求f1（x），f2（x）的表达式；
（2）写出fn（x）的表达式，并用数学归纳法证明．
19．为了调查某区中学教师的工资水平，用分层抽样的方法从初级、中级、高级三个 职称系列的相关教师中抽取若干人，有关数据见下表：
职称类型相关人数抽取人数
初级27x
中级99y
高级182
（1）求x，y值；
（2）若从抽取的初级和离级教师中任选2人，求这2人都是初级教师的概率．
16．已知偶函数y=f（x）在区间[-1，0]上单调递增，且满足f（1-x）+f（1+x）=0，给出下列判断：
①f（-3）=0；②f（x）在[1，2]上是增函数；③f（x）的图象关与直线x=1对称；④函数f（x）在x=2处取得最小值；⑤函数y=f（x）没有最大值，其中判断正确的序号是①④．
3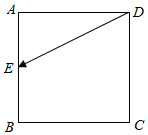．如图所示，已知正方形ABCD的边长为1，点E从D点出发，按字母顺序D→A→B→C沿线段DA，AB，BC运动到C点，在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是（　　）
A．0B．$\frac{1}{2}$C．1D．-1
13．若以连续掷两次骰子分别得到的点数m、n作为点P的横、纵坐标，则点P在直线x+y=6下方的概率是（　　）
A．$\frac{7}{18}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{5}{18}$
20．设变量x，y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$，则M=$\frac{y-x}{x+2}$的取值范围是（　　）
A．[-$\frac{1}{3}$，$\frac{1}{2}$]B．[-$\frac{1}{2}$，1]C．[$\frac{1}{2}$，2]D．[$\frac{2}{3}$，$\frac{3}{2}$]
17．在四面体ABCD内部有一点O，满足OA=OB=OC=4，OD=1，则四面体ABCD体积的最大值为$9\sqrt{3}$．
16．已知函数y=x2-6|x|+2，a-2≤x≤a+2时，函数的最大值为M（a），则M（a）的最值为（　　）
A．2B．-7C．-5D．-3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网