题目内容
11．已知{an}为等差数列，公差为1，且a6是a3与a11的等比中项，Sn是的前n项和，则S12的值为96．分析 由{an}为等差数列，公差为1，且a6是a3与a11的等比中项，可得${a}_{6}^{2}$=a3•a11，即$（{a}_{1}+5）^{2}=（{a}_{1}+2）（{a}_{1}+10）$，解出即可得出．
解答 解：∵{an}为等差数列，公差为1，且a6是a3与a11的等比中项，
∴${a}_{6}^{2}$=a3•a11，
∴$（{a}_{1}+5）^{2}=（{a}_{1}+2）（{a}_{1}+10）$，
解得a1=$\frac{5}{2}$．
S12=$12×\frac{5}{2}$+$\frac{12×11}{2}$×1=96．
故答案为：96．
点评 本题考查了等差数列的通项公式及其前n项和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
3．
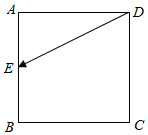如图所示，已知正方形ABCD的边长为1，点E从D点出发，按字母顺序D→A→B→C沿线段DA，AB，BC运动到C点，在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是（ ）
如图所示，已知正方形ABCD的边长为1，点E从D点出发，按字母顺序D→A→B→C沿线段DA，AB，BC运动到C点，在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是（ ）| A． | 0 | B． | $\frac{1}{2}$ | C． | 1 | D． | -1 |
1．命题“?x0≤0，使得x02≥0”的否定是（ ）
| A． | ?x≤0，x2＜0 | B． | ?x≤0，x2≥0 | C． | ?x0＞0，x02＞0 | D． | ?x0＜0，x02≤0 |
8．曲线f（x）=x3-x+3在点P处的切线平行于直线y=2x-1，则P点的坐标为（ ）
| A． | （1，3） | B． | （-1，3） | C． | （1，3）和（-1，3） | D． | （1，-3） |
16．已知函数y=x2-6|x|+2，a-2≤x≤a+2时，函数的最大值为M（a），则M（a）的最值为（ ）
| A． | 2 | B． | -7 | C． | -5 | D． | -3 |
3．A，B是平面α外不同的两个定点，P为平面α内动点，且cos∠PAB=$\frac{1}{3}$，则P点的轨迹是（ ）
| A． | 圆或椭圆 | B． | 抛物线或双曲线 | C． | 椭圆或双曲线 | D． | 以上都有可能 |