题目内容
11.设函数f(x)=3ax2-2(a+b)x+b,x∈[0,1],其中a>0,b为任意常数.若函数f(x)的最大值是a-b,求$\frac{b}{a}$的取值范围.分析 由二次函数的性质可得二次函数f(x)=3ax2-2(a+b)x+b的图象开口向上,且其对称轴为x=$\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$,从而可得|1-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|≥|0-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|,从而解得.
解答 解:∵f(x)=3ax2-2(a+b)x+b,
∴f(1)=3a-2(a+b)+b=a-b,
又∵函数f(x)的最大值是a-b,
函数f(x)=3ax2-2(a+b)x+b在x=1处取得最大值,
又∵a>0,
∴二次函数f(x)=3ax2-2(a+b)x+b的图象开口向上,
且其对称轴为x=$\frac{a+b}{3a}$=$\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$,
∴|1-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|≥|0-($\frac{1}{3}$+$\frac{1}{3}$$\frac{b}{a}$)|,
即$\frac{b}{a}$≤$\frac{1}{2}$.
点评 本题考查了二次函数的性质的判断与应用,同时考查了数形结合的思想应用.

练习册系列答案
相关题目
5.从底面为直角三角形的直三棱柱的9条棱中任取两条,则这两条棱互相垂直的概率为( )
| A. | $\frac{22}{81}$ | B. | $\frac{7}{12}$ | C. | $\frac{11}{18}$ | D. | $\frac{1}{2}$ |
19.为了调查某区中学教师的工资水平,用分层抽样的方法从初级、中级、高级三个 职称系列的相关教师中抽取若干人,有关数据见下表:
(1)求x,y值;
(2)若从抽取的初级和离级教师中任选2人,求这2人都是初级教师的概率.
| 职称类型 | 相关人数 | 抽取人数 |
| 初级 | 27 | x |
| 中级 | 99 | y |
| 高级 | 18 | 2 |
(2)若从抽取的初级和离级教师中任选2人,求这2人都是初级教师的概率.
6.某同学有6本工具书,其中语文1本、英语2本、数学3本,现在他把这6本书放到书架上排成一排,则同学科工具书都排在一起的概率是( )
| A. | $\frac{1}{30}$ | B. | $\frac{1}{15}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{5}$ |
3.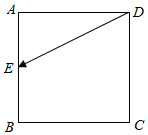 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$,则M=$\frac{y-x}{x+2}$的取值范围是( )
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
1.命题“?x0≤0,使得x02≥0”的否定是( )
| A. | ?x≤0,x2<0 | B. | ?x≤0,x2≥0 | C. | ?x0>0,x02>0 | D. | ?x0<0,x02≤0 |