题目内容
12.已知变量x,y满足$\left\{\begin{array}{l}{x-1≥0}\\{x-y+1≤0}\\{x+y-4≤0}\\{\;}\end{array}\right.$,则$\frac{x}{y+1}$的最小值为$\frac{1}{4}$.分析 画出满足条件的平面区域,求出角点的坐标,结合$\frac{x}{y+1}$的几何意义求出最小值即可.
解答 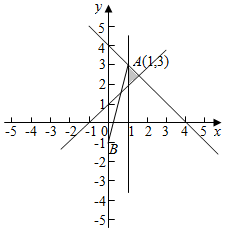 解:画出满足条件的平面区域,如图示:
解:画出满足条件的平面区域,如图示:
,
由$\left\{\begin{array}{l}{x=1}\\{x+y-4=0}\end{array}\right.$,解得A(1,3),
而求$\frac{x}{y+1}$的最小值即为求$\frac{y+1}{x}$的最大值,
$\frac{y+1}{x}$的几何意义表示平面区域内的点与B(0,-1)的直线的斜率,
而KAB=$\frac{3+1}{1}$=4,故$\frac{x}{y+1}$的最小值是:$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查了简单的线性规划问题,考查数形结合思想,是一道中档题.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
3.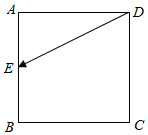 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
 如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )
如图所示,已知正方形ABCD的边长为1,点E从D点出发,按字母顺序D→A→B→C沿线段DA,AB,BC运动到C点,在此过程中$\overrightarrow{DE}•\overrightarrow{CD}$的最大值是( )| A. | 0 | B. | $\frac{1}{2}$ | C. | 1 | D. | -1 |
20.设变量x,y满足约束条件$\left\{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-1≥0}\end{array}\right.$,则M=$\frac{y-x}{x+2}$的取值范围是( )
| A. | [-$\frac{1}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,2] | D. | [$\frac{2}{3}$,$\frac{3}{2}$] |
7.不在3x+2y>3表示的平面区域内的点是( )
| A. | (0,0) | B. | (1,1) | C. | (0,2) | D. | (2,0) |
1.命题“?x0≤0,使得x02≥0”的否定是( )
| A. | ?x≤0,x2<0 | B. | ?x≤0,x2≥0 | C. | ?x0>0,x02>0 | D. | ?x0<0,x02≤0 |