题目内容
若关于x的方程sin2x+2sinx-1+m=0有解.则实数m的范围 .
考点:正弦函数的定义域和值域,二次函数在闭区间上的最值
专题:三角函数的图像与性质
分析:变形换元可得m=-t2-2t+1=-(t+1)2+2,t∈[-1,1],由二次函数区间的最值可得.
解答:
解:∵sin2x+2sinx-1+m=0
∴m=-sin2x-2sinx+1,
令sinx=t,则t∈[-1,1],
∴m=-t2-2t+1=-(t+1)2+2,t∈[-1,1],
由二次函数的知识可知:当t∈[-1,1]时函数单调递减,
∴当t=-1时,函数取最大值2,当t=1时,函数取最小值-2
∴实数m的范围为:-2≤m≤2
故答案为:-2≤m≤2
∴m=-sin2x-2sinx+1,
令sinx=t,则t∈[-1,1],
∴m=-t2-2t+1=-(t+1)2+2,t∈[-1,1],
由二次函数的知识可知:当t∈[-1,1]时函数单调递减,
∴当t=-1时,函数取最大值2,当t=1时,函数取最小值-2
∴实数m的范围为:-2≤m≤2
故答案为:-2≤m≤2
点评:本题考查正弦函数的定义域,涉及二次函数区间的最值,属基础题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
以F(-3,0)为焦点的抛物线的标准方程为( )
| A、y2=6x |
| B、y2=-6x |
| C、y2=12x |
| D、y2=-12x |
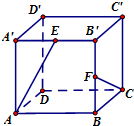 正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为
正方体ABCD-A′B′C′D′中,点E为A1B1的中点,F为B1B的中点,则AE与CF所成角的余弦值为