题目内容

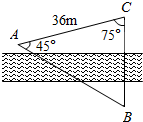如图，在一次测量活动中，要测量河两岸B、C两点间的距离，测量者在河的一侧测得AC=36m，∠BAC=45°，∠BCA=75°，求B、C两点之间的距离．
考点：解三角形的实际应用
专题：应用题,解三角形
分析：先计算B，再利用正弦定理，可求B、C两点之间的距离．
解答： 解：由题意，B=60°，
由正弦定理可得
36
sin60°
=
BC
sin45°
，
∴BC=12
6
m．
点评：本题考查正弦定理，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
向量
a
=（2，3），
b
=（1，2），若
a
+2
b
与m
a
+
b
平行，则m=（　　）
A、-2
B、2
C、-
1
2
D、
1
2
在（1-x）5-（1-x）6的展开式中，含x3的项的系数是（　　）
A、-5B、5C、10D、-10
由抛物线y=x2-x，直线x=-1及x轴围成的图形的面积为（　　）
A、
2
3
B、1
C、
5
6
D、
5
3
如图，该程序运行后输出的结果S为（　　）
A、1B、10C、19D、28
已知点A（2，3），B（1，1）和直线l1：3x-4y+8=0，求
（1）经过点B，且与直线l1平行的直线的方程；
（2）线段AB的垂直平分线的方程．
已知函数f（x）=2cos2x+2sinxcosx．
（Ⅰ）求f（
π
12
）的值；
（Ⅱ）记函数g（x）=f（x-
π
4
）•f（x+
π
4
），若x∈[
π
12
，
π
3
]，求函数g（x）的值域．
设命题p：方程
x2
m+3
-
y2
2-m
=2表示焦点在x轴上的双曲线；命题q：?x∈R，均满足x2+2mx+（m+6）≥0．求使“p且q”为真命题时，实数m的取值范围．
若点A（-1，1），B（1，3），C（x，5）共线，求点C的坐标．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网