题目内容
已知点A(2,3),B(1,1)和直线l1:3x-4y+8=0,求
(1)经过点B,且与直线l1平行的直线的方程;
(2)线段AB的垂直平分线的方程.
(1)经过点B,且与直线l1平行的直线的方程;
(2)线段AB的垂直平分线的方程.
考点:两直线的夹角与到角问题,直线的一般式方程与直线的平行关系
专题:直线与圆
分析:(1)设经过点B,且与直线l1平行的直线的方程为 3x-4y+m=0,把点B的坐标代入求得 m的值,可得所求的直线方程.
(2)先求得线段AB的中点的坐标,直线AB的斜率,可得线段AB的垂直平分线的斜率,再用点斜式求得线段AB的垂直平分线的方程.
(2)先求得线段AB的中点的坐标,直线AB的斜率,可得线段AB的垂直平分线的斜率,再用点斜式求得线段AB的垂直平分线的方程.
解答:
解:(1)设经过点B,且与直线l1平行的直线的方程为 3x-4y+m=0,
把点B的坐标代入可得 3-4+m=0,求得 m=1,故所求的直线方程为3x-4y+1=0.
(2)线段AB的中点为(
,2),直线AB的斜率为
=2,
故线段AB的垂直平分线的斜率为-
,用点斜式求得线段AB的垂直平分线的方程为y-2=-
(x-
),
即 2x+4y-11=0.
把点B的坐标代入可得 3-4+m=0,求得 m=1,故所求的直线方程为3x-4y+1=0.
(2)线段AB的中点为(
| 3 |
| 2 |
| 3-1 |
| 2-1 |
故线段AB的垂直平分线的斜率为-
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
即 2x+4y-11=0.
点评:本题主要考查用待定系数法求直线方程,用点斜式求直线的方程,属于基础题.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
在复平面内,复数z=
(i为虚数单位)等于( )
| 3-i |
| 1+i |
| A、1+2i | B、1-2i |
| C、1+3i | D、-1-3i |
已知函数f′(x)是函数f(x)的导函数,且满足:①
>0;②exf(1-x)-e-xf(1+x)=0,设a=ef(1),b=f(2),c=e3f(-1).则a,b,c的大小顺序为( )
| f(x)-f′(x) |
| x-1 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、b<a>c |
 用6种不同的颜色把图中的A.B.C.D四块区域分开,同一种颜色可以涂不同区域,但相 邻区域不能涂同一种颜色,那么不同的涂色方法种数为( )
用6种不同的颜色把图中的A.B.C.D四块区域分开,同一种颜色可以涂不同区域,但相 邻区域不能涂同一种颜色,那么不同的涂色方法种数为( )| A、400 | B、460 |
| C、480 | D、496 |
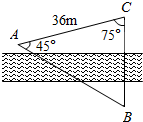 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离. 已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,半径OC与母线PB所成的角的大小等于60°.
已知圆锥母线长为6,底面圆半径长为4,点M是母线PA的中点,AB是底面圆的直径,半径OC与母线PB所成的角的大小等于60°. 根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;
根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;