题目内容
设命题p:方程
-
=2表示焦点在x轴上的双曲线;命题q:?x∈R,均满足x2+2mx+(m+6)≥0.求使“p且q”为真命题时,实数m的取值范围.
| x2 |
| m+3 |
| y2 |
| 2-m |
考点:复合命题的真假
专题:函数的性质及应用
分析:命题p:-3<m<2.命题q:-2≤m≤3.由“p且q”为真命题,得
,由此能求出实数m的取值范围.
|
解答:
解:∵命题p:方程
-
=2表示焦点在x轴上的双曲线,
∴命题p:
,即命题p:-3<m<2.
∵命题q:?x∈R,均满足x2+2mx+(m+6)≥0,
∴命题q:△=4m2-4(m+6)≤0,
即命题q:-2≤m≤3.
∵“p且q”为真命题,
∴
,解得-2≤m<2.
∴实数m的取值范围是[-2,2).
| x2 |
| m+3 |
| y2 |
| 2-m |
∴命题p:
|
∵命题q:?x∈R,均满足x2+2mx+(m+6)≥0,
∴命题q:△=4m2-4(m+6)≤0,
即命题q:-2≤m≤3.
∵“p且q”为真命题,
∴
|
∴实数m的取值范围是[-2,2).
点评:本题考查实数的取值范围的求法,是基础题,解题时要认真审题,注意双曲线、一元二次不等式等知识点的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在复平面内,复数z=
(i为虚数单位)的共轭复数对应的点位于( )
| i |
| 3-4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
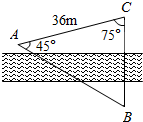 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离. 根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;
根据如图所示的程序框图,将输出的x、y值依次分别记为x1,x2,…,xn,…,x2007;y1,y2,…,yn…,y2007;