题目内容
由抛物线y=x2-x,直线x=-1及x轴围成的图形的面积为( )
A、
| ||
| B、1 | ||
C、
| ||
D、
|
考点:定积分在求面积中的应用
专题:计算题,导数的概念及应用
分析:联立两个曲线的方程,判断他们的交点,以确定积分公式中x的取值范围,再根据定积分的几何意义,即得答案.
解答:
解:由抛物线y=x2-x,直线x=-1,得交点坐标是(-1,2),
∴抛物线y=x2-x,直线x=-1及x轴围成的图形的面积为S=
(x2-x)dx=(
x3-
x2)
=
.
故选:C.
∴抛物线y=x2-x,直线x=-1及x轴围成的图形的面积为S=
| ∫ | 0 -1 |
| 1 |
| 3 |
| 1 |
| 2 |
| | | 0 -1 |
| 5 |
| 6 |
故选:C.
点评:此题考查了定积分的运算,利用定积分表示封闭图形的面积是解本题的关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案
相关题目
从5种不同的书(每种书不少于3本)买3本送给3名同学,每人各一本的不同送法有( )
A、A
| ||||
| B、53 | ||||
| C、35 | ||||
D、A
|
在复平面内,复数z=
(i为虚数单位)的共轭复数对应的点位于( )
| i |
| 3-4i |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知函数f′(x)是函数f(x)的导函数,且满足:①
>0;②exf(1-x)-e-xf(1+x)=0,设a=ef(1),b=f(2),c=e3f(-1).则a,b,c的大小顺序为( )
| f(x)-f′(x) |
| x-1 |
| A、a>b>c |
| B、a>c>b |
| C、b>c>a |
| D、b<a>c |
阅读程序框图,执行相应的程序,若输入x=4,则输出y的值为( )


A、-
| ||
B、-
| ||
C、-
| ||
D、-
|
 用6种不同的颜色把图中的A.B.C.D四块区域分开,同一种颜色可以涂不同区域,但相 邻区域不能涂同一种颜色,那么不同的涂色方法种数为( )
用6种不同的颜色把图中的A.B.C.D四块区域分开,同一种颜色可以涂不同区域,但相 邻区域不能涂同一种颜色,那么不同的涂色方法种数为( )| A、400 | B、460 |
| C、480 | D、496 |
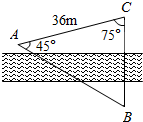 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧测得AC=36m,∠BAC=45°,∠BCA=75°,求B、C两点之间的距离.