题目内容
若两条曲线的极坐标方程分别为ρ＝1与ρ＝2cos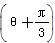
，它们相交于A、B两点，求线段AB的长．
解：(解法1)联立方程
得交点坐标为A(1，0)，B
(注意坐标形式不唯一)．在△OAB中，根据余弦定理，得AB2＝1＋1－2×1×1×cos
＝3，所以AB＝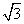
.
(解法2)由ρ＝1，得x2＋y2＝1.
∵ ρ＝2cos
＝cosθ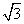－sinθ，∴ ρ2＝ρcosθ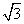－·ρsinθ，
∴ x2＋y2－x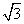＋y＝0.
由
得A(1，0)、B
，
∴AB＝
＝.
练习册系列答案
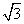名题金卷系列答案
相关题目
时，f(x)≤g(x)，求a的取值范围．
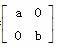(其中a>0，b>0)．
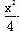＋y2＝1，求a、b的值．
(θ为参数)交于点A、B，求PA·PB的值．
，圆心为直线ρsin
＝－
与极轴的交点，求圆C的极坐标方程．
，求AF的长．
