题目内容
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1时,且当x∈ 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
解析: (1)当a=-2时,不等式f(x)<g(x)化为|2x-1|+|2x-2|-x-3<0.
设函数y=|2x-1|+|2x-2|-x-3,
 则y=
则y=
其图象如图所示,由图象可知,当且仅当x∈(0,2)时,y<0,所以原不等式的解集是{x|0<x<2}.
(2)当x∈ 时,f(x)=1+a,
时,f(x)=1+a,
不等式f(x)≤g(x)化为1+a≤x+3,
所以x≥a-2对x∈ 都成立,故-
都成立,故- ≥a-2,即a≤
≥a-2,即a≤ .
.
从而a的取值范围是 .
.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
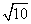 ,则|b|=( )
,则|b|=( )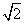 B.2
B.2 ,N=
,N= +
+ ,求M与N的大小关系.
,求M与N的大小关系.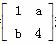 对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值.
对应的变换作用下得到直线m:x-y-4=0,求实数a、b的值. 所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.
所对应的线性变换把点A(x,y)变成点A′(13,5),试求M的逆矩阵及点A的坐标.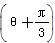 ,它们相交于A、B两点,求线段AB的长.
,它们相交于A、B两点,求线段AB的长.