题目内容
设矩阵M＝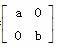
(其中a>0，b>0)．
(1) 若a＝2，b＝3，求矩阵M的逆矩阵M－1；
(2) 若曲线C：x2＋y2＝1在矩阵M所对应的线性变换作用下得到曲线C′：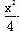
＋y2＝1，求a、b的值．
解：(1) 设矩阵M的逆矩阵M－1＝
，则MN－1＝
，所以
，所以2x1＝1，2y1＝0，3x2＝0，3y2＝1，即x1＝
，y1＝0，x2＝0，y2＝
，故所求的逆矩阵M－1＝
(2) 设曲线C上任意一点P(x，y)，它在矩阵M所对应的线性变换作用下得到P′(x′，y′)，则
又点P′(x′，y′)在曲线C′上，所以
＋y′2＝1，则
＋b2y2＝1为曲线C的方程．又已知曲线C的方程为x2＋y2＝1，故
又a>0，b>0，所以
练习册系列答案
相关题目
，N＝
＋
，求M与N的大小关系．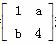
对应的变换作用下得到直线m：x－y－4＝0，求实数a、b的值．
所对应的线性变换把点A(x，y)变成点A′(13，5)，试求M的逆矩阵及点A的坐标．
，求矩阵A－1B.
(t为参数)与直线l2：2x－4y＝5相交于点B，又点A(1，2)，求|AB|.
(t为参数)，求曲线C1和C2的交点坐标．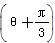
，它们相交于A、B两点，求线段AB的长．