题目内容
若点G为△AOB的中线OM的中点，过点G作直线分别交OA，OB与点平P，Q．设
=m，
=n，则
+
的值为（ ）
| OP |
| OA |
| OQ |
| OB |
| 1 |
| m |
| 1 |
| n |
| A、4 | ||
| B、1 | ||
C、
| ||
| D、2 |
考点：函数恒成立问题
专题：函数的性质及应用,平面向量及应用
分析：向量法：由三点P，G，Q共线，可得存在实数λ满足
=λ
+（1-λ）
，由向量运算可得
=
（
+
），又可得
=λm
+（1-λ）n
，对应系数相等可得方程组，变形可得答案．
| OG |
| OP |
| OQ |
| OG |
| 1 |
| 4 |
| OA |
| OB |
| OG |
| OA |
| OB |
解答：
解：（如图）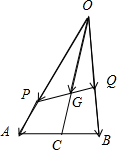
∵三点P，G，Q共线，
∴存在实数λ满足
=λ
+（1-λ）
，
∵点G为△AOB的中线OM的中点，
∴
=
=
×
（
+
）=
（
+
），
又∵
=m，
=n，∴
=m
，
=n
，
∴
=λ
+（1-λ）
=λm
+（1-λ）n
，
∴
，∴
+
=λ+1-λ=1，
∴
+
=4
故选：A
∵三点P，G，Q共线，∴存在实数λ满足
| OG |
| OP |
| OQ |
∵点G为△AOB的中线OM的中点，
∴
| OG |
| 1 |
| 2 |
| OC |
| 1 |
| 2 |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 4 |
| OA |
| OB |
又∵
| OP |
| OA |
| OQ |
| OB |
| OP |
| OA |
| OQ |
| OB |
∴
| OG |
| OP |
| OQ |
| OA |
| OB |
∴
|
| 1 |
| 4m |
| 1 |
| 4n |
∴
| 1 |
| m |
| 1 |
| n |
故选：A
点评：本题考查函数恒成立问题，转化为向量利用平面向量基本定理是解决问题的关键，属难题．
练习册系列答案
相关题目
已知集合A={x|x=2n，n∈Z}，B={x|x=2n+1，n∈Z}，i是虚数单位，若k∈Z且ik∈{-1，1}，则（ ）
| A、k∈A | B、k∈B |
| C、k∈A∩B | D、k∈∅ |
以直角坐标系的原点为极点，x轴的正半轴为极轴建立极坐标系，并在两坐标系中取相同的长单位，曲线C的参数方程为
（参数θ∈[0，π]），直线l的极坐标方程为ρ（cosθ-sinθ）=1．则在C上到直线l距离分别为
和3
的点共有（ ）
|
| 2 |
| 2 |
| A、1个 | B、2个 | C、3个 | D、4个 |
如果数据x1，x2，x3，…xn的平均数为
，方差为s2，则：数据3x1+5，3x2+5，3x3+5，…3xn+5的平均数和方差分别是（ ）
. |
| x |
A、
| ||
B、3
| ||
C、3
| ||
D、3
|