题目内容
在△ABC中,已知a=
,b=
,B=45°,求∠A、∠C和c.
| 3 |
| 6 |
考点:正弦定理
专题:解三角形
分析:由已知及正弦定理可解得sinA的值,故根据大边对大角可得A=30°,即可求C=180°-45°-30°的值,从而由正弦定理可求得c=
的值.
| asinC |
| sinA |
解答:
解:由正弦定理可得:sinA=
=
=
,
由在△ABC中,已知a=
<b=
,
故根据大边对大角可得:A为锐角,
故解得:A=30°.
故C=180°-45°-30°=105°,
从而由正弦定理可得:c=
=
=
.
| asinB |
| b |
| ||
|
| 1 |
| 2 |
由在△ABC中,已知a=
| 3 |
| 6 |
故根据大边对大角可得:A为锐角,
故解得:A=30°.
故C=180°-45°-30°=105°,
从而由正弦定理可得:c=
| asinC |
| sinA |
| ||
| sin30° |
3
| ||||
| 2 |
点评:本题主要考查了正弦定理的应用,考查了大边对大角知识的应用,属于基本知识的考查.

练习册系列答案
相关题目
设集合A={x|x2<4,x∈Z},B={x|x≤3,x∈N},定义A•B={(x,y)|x∈A∩B,y∈A∪B},则A•B的非空真子集的个数共有( )
| A、8 | B、10 |
| C、1024 | D、1022 |
已知集合A={x||x|<1},B={x|2x>1},则A∩B=( )
| A、(-1,0) | ||
| B、(-1,1) | ||
C、(0,
| ||
| D、(0,1) |
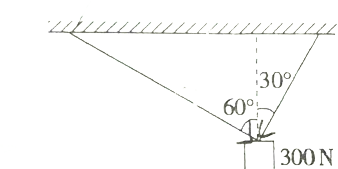 如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力.
如图所示,在重300N的物体上拴两根绳子,这两根绳子在铅垂线的两侧,与铅垂线的夹角分别为30°,60°,当整个系统处于平衡状态时,求两根绳子的拉力. 设
设