题目内容
设集合A={x|x2<4,x∈Z},B={x|x≤3,x∈N},定义A•B={(x,y)|x∈A∩B,y∈A∪B},则A•B的非空真子集的个数共有( )
| A、8 | B、10 |
| C、1024 | D、1022 |
考点:子集与真子集
专题:集合
分析:根据所给的两个集合的元素,写出两个集合的交集与并集,根据新定义的集合规则,得到x和y分别有2和5种结果,根据分步计数原理得新集合中元素的个数,
得到集合的子集的个数是2的元素个数次方,再排除空集和它本身,即可得到真子集的个数.
得到集合的子集的个数是2的元素个数次方,再排除空集和它本身,即可得到真子集的个数.
解答:
解:∵A={x|x2<4,x∈Z}={-1,0,1},B={x|x≤3,x∈N}={0,1,2,3},
∴A∩B={0,1},A∪B={-1,0,1,2,3}
∵A•B={(x,y)|x∈A∩B,y∈A∪B},
x有2种取法,
y有5种取法
∴根据乘法原理得2×5=10,
∴集合A•B的元素的个位有10个,
∴集合A•B的非空真子集的个数,210-2=1022
故选:D
∴A∩B={0,1},A∪B={-1,0,1,2,3}
∵A•B={(x,y)|x∈A∩B,y∈A∪B},
x有2种取法,
y有5种取法
∴根据乘法原理得2×5=10,
∴集合A•B的元素的个位有10个,
∴集合A•B的非空真子集的个数,210-2=1022
故选:D
点评:本题考查了集合间的关系,比较简单,正确求出集合A∩B和A∪B是解题的关键,属于基础题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
如图是一个四棱锥在空间直角坐标系xoz、xoy、yoz三个平面上的正投影,则此四棱锥的体积为( )
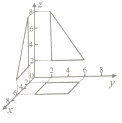

| A、94 | B、32 | C、64 | D、16 |