题目内容
 设
设| a |
| 3 |
| b |
| a |
| b |
(1)求函数f(x)的最小正周期;
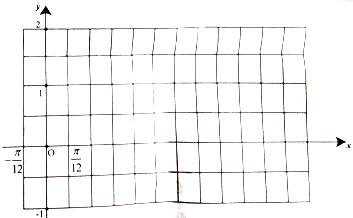
(2)试用“五点法”画出函数f(x)在区间[-
| π |
| 12 |
| 11π |
| 12 |
(3)若对任意x∈[-
| π |
| 6 |
| π |
| 3 |
考点:五点法作函数y=Asin(ωx+φ)的图象,平面向量数量积的运算
专题:作图题,函数的性质及应用,三角函数的图像与性质,平面向量及应用
分析:(1)先利用向量数量积的坐标运算写出函数f(x)的解析式,再利用二倍角公式和两角和的正弦公式将函数化简为y=Asin(ωx+φ)的形式,最后由周期公式即可得f(x)的最小正周期;
(2)由(1)f(x)=sin(2x+
)+
,利用五点法,即将2x+
看成整体取正弦函数的五个关键点,通过列表、描点、连线画出函数图象;
(3)令g(x)=f(x)-m,由x的范围,求得g(x)的最小值,再求f(0),由任意x∈[-
,
]时,不等式f(x)-m≥f(0)恒成立,即有f(0)不大于最小值,解不等式即可得到m的范围.
(2)由(1)f(x)=sin(2x+
| π |
| 6 |
| 1 |
| 2 |
| π |
| 6 |
(3)令g(x)=f(x)-m,由x的范围,求得g(x)的最小值,再求f(0),由任意x∈[-
| π |
| 6 |
| π |
| 3 |
解答:
解:(1)
=(
sinx,cosx),
=(cosx,cosx),
则f(x)=
•
=
sinxcosx+cos2x=
sin2x+
=sin(2x+
)+
则函数f(x)的最小正周期T=
=π;
(2)先列表,再描点连线,可得简图.

(3)令g(x)=f(x)-m=sin(2x+
)+
-m,
∵x∈[-
,
],
∴2x+
∈[-
,
]
∴sin(2x+
)∈[-
,1],
∴g(x)∈[-m,
-m],
当2x+
=-
即x=-
时,g(x)取得最小值-m,
又f(0)=
+
=1,
对任意x∈[-
,
]时,不等式f(x)-m≥f(0)恒成立,
则1≤-m,即有m≤-1.
故实数m的取值范围是(-∞,-1].
| a |
| 3 |
| b |
则f(x)=
| a |
| b |
| 3 |
| ||
| 2 |
| 1+cos2x |
| 2 |
=sin(2x+
| π |
| 6 |
| 1 |
| 2 |
则函数f(x)的最小正周期T=
| 2π |
| 2 |
(2)先列表,再描点连线,可得简图.
| x | -
|
|
|
|
| ||||||||||
2x+
| 0 |
| π |
| 2π | ||||||||||
sin(2x+
| 0 | 1 | 0 | -1 | 0 | ||||||||||
| y |
|
|
| -
|
|

(3)令g(x)=f(x)-m=sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∵x∈[-
| π |
| 6 |
| π |
| 3 |
∴2x+
| π |
| 6 |
| π |
| 6 |
| 5π |
| 6 |
∴sin(2x+
| π |
| 6 |
| 1 |
| 2 |
∴g(x)∈[-m,
| 3 |
| 2 |
当2x+
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
又f(0)=
| 1 |
| 2 |
| 1 |
| 2 |
对任意x∈[-
| π |
| 6 |
| π |
| 3 |
则1≤-m,即有m≤-1.
故实数m的取值范围是(-∞,-1].
点评:本题综合考查了向量的数量积的坐标表示及三角变换公式的运用,三角函数的图象画法,及复合三角函数值域的求法,同时考查不等式的恒成立问题转化为求函数的最值问题,属于中档题.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
 一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是1的圆,则这个几何体的体积是( )
一个几何体的三视图如图所示,其中俯视图与侧视图均为半径是1的圆,则这个几何体的体积是( )A、
| ||
B、
| ||
| C、π | ||
D、
|
如图,点D是线段BC的中点,BC=6,且|
+
|=|
-
|,则|
|=( )

| AB |
| AC |
| AB |
| AC |
| AD |

A、
| ||
B、2
| ||
| C、3 | ||
| D、6 |
 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DA,E,F分别是AB,PB的中点.