Question

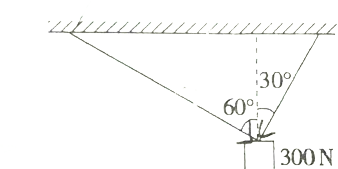如图所示，在重300N的物体上拴两根绳子，这两根绳子在铅垂线的两侧，与铅垂线的夹角分别为30°，60°，当整个系统处于平衡状态时，求两根绳子的拉力．

Answer 1

考点：平面向量数量积的含义与物理意义

专题：方程思想,平面向量及应用

分析：根据题意，画出图形，结合图形，利用平衡力的特征，列出方程组，求出两根绳子的拉力．

解答： 解：如图所示，
根据平衡力的特征，两根绳子的拉力F₁、F₂与重力G是平衡力；
∴F₁sin30°=F₂sin60°①，
F₁cos30°+F₂cos60°=G②；
即

1 2 F1= 3 2 F2 3 2 F1+ 1 2 F2=300

，
解得F₂=150，F₁=150

3

；
∴这两根绳子的拉力分别为150

3

N和150N．

点评：本题考查了平面向量的几何意义的应用问题，是基础题目．