题目内容
已知椭圆M:
+
=1(a>b>0)过(1,
),e=
,直线l1:y=kx+m(m≠0)与椭圆交于AB两点,直线l2:y=kx-m与椭圆交于C、D两点.
(1)求椭圆的方程;
(2)当k=1时,求四边形ABCD面积的最大值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| ||
| 2 |
(1)求椭圆的方程;
(2)当k=1时,求四边形ABCD面积的最大值.
考点:椭圆的标准方程
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)利用待定系数法,建立方程组,求出a,b,即可求椭圆的方程;
(2)当k=1时,四边形ABCD是平行四边形,表示出两平行线AB,CD间的距离,|AB|,可得面积,再利用配方法,求四边形ABCD面积的最大值.
(2)当k=1时,四边形ABCD是平行四边形,表示出两平行线AB,CD间的距离,|AB|,可得面积,再利用配方法,求四边形ABCD面积的最大值.
解答:
解:(1)由题意得
,解得a=2,b=1,
所以椭圆方程为
+y2=1;
(2)由题意知直线l1和直线l2关于原点对称,则AB=CD,所以四边形ABCD是平行四边形,
设两平行线AB,CD间的距离为d,则d=
=
|m|.
y=x+m代入
+y2=1,整理可得5x2+8mx+4m2-4=0,
设A、B两点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=-
,x1x2=
,
∴|AB|=
•
所以S=
•
•
|m|=
≤4
所以四边形ABCD的面积S取得最大值为4.
|
所以椭圆方程为
| x2 |
| 4 |
(2)由题意知直线l1和直线l2关于原点对称,则AB=CD,所以四边形ABCD是平行四边形,
设两平行线AB,CD间的距离为d,则d=
| |m-(-m)| | ||
|
| 2 |
y=x+m代入
| x2 |
| 4 |
设A、B两点的坐标分别为(x1,y1),(x2,y2),
则x1+x2=-
| 8m |
| 5 |
| 4m2-4 |
| 5 |
∴|AB|=
| 2 |
(
|
所以S=
| 2 |
(
|
| 2 |
| 8 |
| 5 |
-(m2-
|
所以四边形ABCD的面积S取得最大值为4.
点评:本题考查椭圆方程,考查直线与椭圆的位置关系,考查学生的计算能力,正确运用韦达定理是关键.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
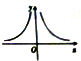 已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )
已知幂函数f(x)=xn-2(n∈N)的图象如图所示,则y=f(x)在x=1处的切线与两坐标轴围成的面积为( )A、
| ||
B、
| ||
C、
| ||
| D、4 |