题目内容
已知e为自然对数的底数,设函数f(x)=(ex-1)(x-1)k(k=1,2),则( )
A.当k=1时,f(x)在x=1处取到极小值
B.当k=1时,f(x)在x=1处取到极大值
C.当k=2时,f(x)在x=1处取到极小值
D.当k=2时,f(x)在x=1处取到极大值
C
[解析] ①当k=1时,f(x)=(ex-1)(x-1),此时f ′(x)=ex(x-1)+(ex-1)=ex·x-1,∴A、B项均错.②当k=2时,f(x)=(ex-1)(x-1)2此时f ′(x)=ex(x-1)2+(2x-2)(ex-1)=ex·x2-2x-ex+2=ex(x+1)(x-1)-2(x-1)=(x-1)[ex(x+1)-2],显然f ′(1)=0,x>1时f ′(x)>0,x<1时,在x=1附近x-1<0,ex(x+1)>2,∴f ′(x)<0,故f(x)在x=1处取得极小值.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
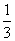 x3-
x3- ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.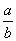 B.
B.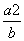 C.
C.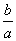 D.
D.
 lnxdx=( )
lnxdx=( )