题目内容
若函数f(x)=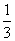 x3-
x3- ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
ax2+(a-1)x+1在区间(1,4)上为减函数,在区间(6,+∞)上为增函数,试求实数a的取值范围.
函数f(x)的导数f ′(x)=x2-ax+a-1.
令f ′(x)=0,解得x=1,或x=a-1.
当a-1≤1即a≤2时,函数f(x)在(1,+∞)上为增函数,不合题意;
当a-1>1即a>2时,函数f(x)在(-∞,1)上为增函数,在(1,a-1)上为减函数,在(a-1,+∞)上为增函数.
依题意当x∈(1,4)时,f ′(x)<0;
当x∈(6,+∞)时,f ′(x)>0.
所以4≤a-1≤6,解得5≤a≤7.
所以a的取值范围为[5,7].

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
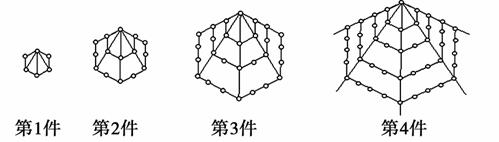
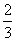 ,2);
,2);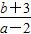 的取值范围是( )
的取值范围是( )
 )∪(3,+∞)
)∪(3,+∞) ,3)
,3) 中,已知
中,已知 =
= ,
, =
= ,
, 为
为 边的中点,则下列向量与
边的中点,则下列向量与 同向的是
同向的是 B.
B.  C.
C.  D.
D. 