题目内容
14.点P在抛物线y2=4x上运动,点Q在直线x-y+5=0上运动,直线l是抛物线的准线,设点P到直线l的距离为d,则d+|PQ|的最小值为( )| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 6 |
分析 由抛物线的性质可知:|PF|+|PQ|的最小值为点F(1,0)到直线x-y+5=0的距离,根据点到直线的距离公式即可求得:d+|PQ|的最小值.
解答 解:抛物线y2=4x的焦点坐标为F(1,0),
由题意可得:|PF|+|PQ|的最小值为点F(1,0)到直线x-y+5=0的距离,
$\frac{|1+5|}{\sqrt{2}}$=3$\sqrt{2}$.
故选:C.
点评 本题考查抛物线的性质,考查点到直线的距离公式,属于中档题.

练习册系列答案
相关题目
2.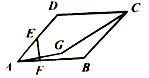 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
 如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )
如图所示,四边形ABCD是菱形,边长为2,∠BAD=60°,E为边AD的中点,点F在边AB上运动,点A关于直线EF的对称点为G,则线段CG的长度最小值为( )| A. | $\sqrt{7}-1$ | B. | 2 | C. | $\sqrt{5}-1$ | D. | $\sqrt{3}$ |
9.某单位有职工200名,现要从中抽取40名职工作样本,用系统抽样法,将全体职工随机按1-200编号,并按编号顺序平均分为40组.若第5组抽出的号码为22,则第10组抽出的号码应是( )
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
19.已知复数z=x+yi,满足|z-3-4i|=1,则x2+y2的取值范围是( )
| A. | [4,6] | B. | [5,6] | C. | [25,36] | D. | [16,36] |
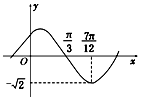 (1)求$f(x)=tan(3x-\frac{π}{4})$的定义域
(1)求$f(x)=tan(3x-\frac{π}{4})$的定义域