Question

2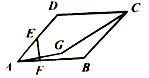．如图所示，四边形ABCD是菱形，边长为2，∠BAD=60°，E为边AD的中点，点F在边AB上运动，点A关于直线EF的对称点为G，则线段CG的长度最小值为（　　）

• A． $\sqrt{7}-1$
• B． 2
• C． $\sqrt{5}-1$
• D． $\sqrt{3}$

Answer 1

分析 由题意画出图形，可知当F在线段AB上运动时，A关于EF的对称点G到E的距离都等于定值EA=1，由余弦定理求出CE，用CF减去1得答案．

解答 解：如图，
当F在线段AB上运动时，A关于EF的对称点G到E的距离都等于定值EA=1，
∵ED=1，CD=2，∠CDE=120°，
∴$CE=\sqrt{{1}^{2}+{2}^{2}-2×1×2×cos120°}=\sqrt{7}$．
∴当A关于EF的对称点G落在EC上时，CG最小为$\sqrt{7}-1$．
故选：A．

点评 本题考查向量在几何中的应用，考查数学转化思想方法，考查了思维能力，是中档题．