题目内容
4. (1)求$f(x)=tan(3x-\frac{π}{4})$的定义域
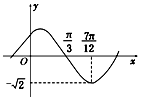
(1)求$f(x)=tan(3x-\frac{π}{4})$的定义域(2)函数f(x)=Asin(ωx+φ)(A,ω,φ为常数,A>0,ω>0)的部分图象如图所示,求f(0).
分析 (1)根据正切函数的定义,令3x-$\frac{π}{4}$≠kπ+$\frac{π}{2}$求出x的取值范围即可;
(2)由图象求出函数的解析式,再计算f(0)的值.
解答 解:(1)∵f(x)=tan(3x-$\frac{π}{4}$),
∴3x-$\frac{π}{4}$≠kπ+$\frac{π}{2}$,k∈Z;
解得x≠$\frac{kπ}{3}$+$\frac{π}{4}$,k∈Z;
故函数f(x)=tan(3x-$\frac{π}{4}$)的定义域为{x|x≠$\frac{kπ}{3}$+$\frac{π}{4}$,k∈Z};
(2)由图可知,A=$\sqrt{2}$,$\frac{T}{4}$=$\frac{7π}{12}$-$\frac{π}{3}$=$\frac{π}{4}$,
∴T=π,又T=$\frac{2π}{ω}$(ω>0),
∴ω=2.
又函数图象经过点($\frac{π}{3}$,0),
∴2×$\frac{π}{3}$+φ=2kπ+π,
∴φ=2kπ+$\frac{π}{3}$(k∈Z),
∴函数的解析式为:f(x)=$\sqrt{2}$sin(2x+$\frac{π}{3}$),
∴f(0)=$\sqrt{2}$sin$\frac{π}{3}$=$\frac{\sqrt{6}}{2}$.
点评 本题考查了三角函数的定义、图象与性质的应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
14.点P在抛物线y2=4x上运动,点Q在直线x-y+5=0上运动,直线l是抛物线的准线,设点P到直线l的距离为d,则d+|PQ|的最小值为( )
| A. | 4 | B. | 2$\sqrt{3}$ | C. | 3$\sqrt{2}$ | D. | 6 |
15.已知集合A={x|ax2+2x+a=0,a∈R},若集合A有且仅有2个子集,则实数a的取值组成的集合为( )
| A. | {-1,0} | B. | {0,1} | C. | {-1,1} | D. | {-1,0,1} |
9.圆锥的底面半径为1,母线长为2,顶点为S,轴截面为△SAB,C为SB的中点.若由A点绕侧面至点C,则最短路线长为( )
| A. | $\sqrt{7}$ | B. | 3 | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |