题目内容
下列函数中既不是奇函数,又不是偶函数的是( )
| A、y=2|x| | ||
| B、y=2x+2-x | ||
C、y=lg
| ||
D、y=lg(x+
|
考点:函数奇偶性的判断
专题:函数的性质及应用
分析:A.y=2|x|是偶函数;
B.y=2x+2-x是奇函数;
C.y=lg
的定义域为x>-1,关于原点不对称.
D.y=lg(x+
),其定义域为R,且f(-x)+f(x)=lg1=0.
B.y=2x+2-x是奇函数;
C.y=lg
| 1 |
| x+1 |
D.y=lg(x+
| x2+1 |
解答:
解:A.y=2|x|是偶函数;
B.y=2x+2-x是奇函数;
C.y=lg
的定义域为x>-1,关于原点不对称,因此既不是奇函数,又不是偶函数.
D.y=lg(x+
),其定义域为R,且f(-x)+f(x)=lg1=0,因此是奇函数.
故选:C.
B.y=2x+2-x是奇函数;
C.y=lg
| 1 |
| x+1 |
D.y=lg(x+
| x2+1 |
故选:C.
点评:本题查克拉函数的奇偶性,属于基础题.

练习册系列答案
相关题目
已知点P在直线AB上,点O不在直线AB上,且存在实数t满足
=2t
+t
,则
=( )
| OP |
| PA |
| OB |
|
| ||
|
|
A、
| ||
B、
| ||
| C、2 | ||
| D、3 |
方程x
-(
)x-2=0的解所在的区间为( )
| 1 |
| 3 |
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
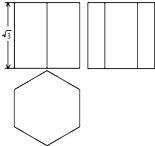 如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )
如图是一个六棱柱的三视图,俯视图是一个周长为3的正六边形,该六棱柱的顶点都在同一个球面上,那么这个球的体积为( )A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=
的定义域是( )
| ||
| lgx-1 |
| A、[4,+∞) |
| B、(10,+∞) |
| C、(4,10)∪(10,+∞) |
| D、[4,10)∪(10,+∞) |
某储蓄所计划从2011年起,力争做到每年的吸储量比前一年增长8%,则到2014年底该储蓄所的吸储量将比2011年的吸储量增加( )
| A、24% |
| B、32% |
| C、(1.083-1)×100% |
| D、(1.084-1)×1.083 |
若a≠b,数列a,x1,x2,b和数列a,y1,y2,y3,b都是等差数列,则
=( )
| x2-x1 |
| y2-y1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
已知函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-2或6 | ||
B、-2或
| ||
| C、-2或2 | ||
D、2或
|