题目内容
设f(x)= sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
[2,+∞)
[解析] 本题考查了三角函数中两角和的正弦公式的逆用.
由f(x)= sin3x+cosx=2(
sin3x+cosx=2(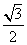 sin3x+
sin3x+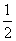 cos3x)
cos3x)
=2sin(3x+ ),所以|f(x)|≤2,所以a≥2.
),所以|f(x)|≤2,所以a≥2.
本题也可直接利用辅助角公式asinx+bcosx= sin(x+φ)得到|f(x)|最大值.
sin(x+φ)得到|f(x)|最大值.

练习册系列答案
相关题目
题目内容
设f(x)= sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
[2,+∞)
[解析] 本题考查了三角函数中两角和的正弦公式的逆用.
由f(x)= sin3x+cosx=2(
sin3x+cosx=2(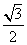 sin3x+
sin3x+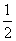 cos3x)
cos3x)
=2sin(3x+ ),所以|f(x)|≤2,所以a≥2.
),所以|f(x)|≤2,所以a≥2.
本题也可直接利用辅助角公式asinx+bcosx= sin(x+φ)得到|f(x)|最大值.
sin(x+φ)得到|f(x)|最大值.
