题目内容
已知函数f(x)=4cosωx·sin(ωx+ )(ω>0)的最小正周期为π
)(ω>0)的最小正周期为π
(1)求ω的值;
(2)讨论f(x)在区间[0, ]上的单调性.
]上的单调性.
[解析] (1)f(x)=4cosωx·sin(ωx+ )
)
=2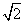 sinxω·cosωx+2
sinxω·cosωx+2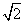 cos2ωx
cos2ωx
=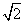 (sin2ωx+cos2ωx)+
(sin2ωx+cos2ωx)+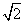 =2sin(2ωx+
=2sin(2ωx+ )+
)+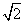 .
.
因为f(x)的最小正周期为π,且ω>0,
从而有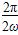 =π,故ω=1.
=π,故ω=1.
(2)由(1)知f(x)=2sin(2x+ )+
)+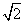 .
.
若0≤x≤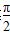 ,则
,则 ≤2x+
≤2x+ ≤
≤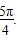
当 ≤2x+
≤2x+ ≤
≤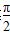 ,即0≤x≤
,即0≤x≤ 时,f(x)单调递增;
时,f(x)单调递增;
当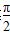 ≤2x+
≤2x+ ≤
≤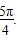 ,即
,即 ≤x≤
≤x≤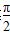 时,f(x)单调递减.
时,f(x)单调递减.
综上可知,f(x)在区间[0, ]上单调递增,
]上单调递增,
在区间[ ,
,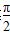 ]上单调递减.
]上单调递减.

练习册系列答案
相关题目
 B.
B.
 D.
D.
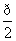 以后,所得到的图像的函数式是y=sin(x+
以后,所得到的图像的函数式是y=sin(x+ ),则原来的函数表达式为( )
),则原来的函数表达式为( ) ) B.y=sin(x+
) B.y=sin(x+ )
) ) D.y=sin(x+
) D.y=sin(x+ sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________.
sin3x+cos3x,若对任意实数x都有|f(x)|≤a,则实数a的取值范围是________. 的对称中心是____________.
的对称中心是____________. 定
定
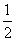 >0.则命题“p∧(綈q)”是假命题;
>0.则命题“p∧(綈q)”是假命题;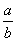 =-3;
=-3;