题目内容
设函数f(x)＝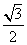
－
sin2ωx－sinωxcosωx(ω>0)，且y＝f(x)图像的一个对称中心到最近的对称轴的距离为
(1)求ω的值；
(2)求f(x)在区间[π，
]上的最大值和最小值．
(1)f(x)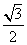＝－sin2ωx－sinωxcosωx
＝－·
－
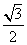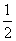sin2ωx
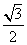＝cos2ωx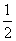－sin2ωx
＝－sin(2ωx－
)．
因为图像的一个对称中心到最近的对称轴的距离为
，
又ω>0，所以
＝4×
，
因此ω＝1.
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
，Q＝
(lga＋lgb)，R＝lg
，则( )
＝a1a4－a2a3.将函数f(x)＝
的图像向左平移
个单位，以下是所得函数图像的一个对称中心的是( )
定
，
，
，
，
，
，…，
，
，…，
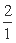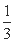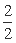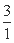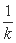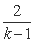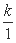，…，在这个数列中，第50个值等于1的项的序号是（ ）
(A，c为常数)．已知工人组装第4件产品用时30分钟，组装第A件产品用时15分钟，那么c和A的值分别是( )