题目内容
16.已知a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$,若z=2x+y的最小值为1,则a=( )| A. | 1 | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | 2 |
分析 画出约束条件的可行域,利用目标函数的最值判断最优解,利用直线方程求解即可.
解答 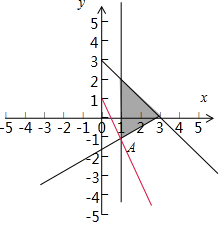 解:a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$的可行域如图:
解:a>0,x,y满足约束条件$\left\{\begin{array}{l}{x≥1}\\{x+y≤3}\\{y≥a(x-3)}\end{array}\right.$的可行域如图:
且目标函数z=2x+y的最小值为1,可知目标函数经过可行域的A时,取得最小值,
由$\left\{\begin{array}{l}{x=1}\\{2x+y=1}\end{array}\right.$解得A(1,-1),A在直线y=a(x-3)上,
可得-1=a(1-3),解得a=$\frac{1}{2}$,
故选:C.
点评 本题考查线性规划的简单应用,目标函数的最值与可行域的关系是解题的关键,考查计算能力.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
7.已知边长为2的正三角形ABC,P,M满足|AP|=1,$\overrightarrow{PM}$=$\overrightarrow{MC}$,则$\overrightarrow{BM}$2的最小值是( )
| A. | $\frac{9-2\sqrt{3}}{4}$ | B. | $\frac{11-3\sqrt{3}}{4}$ | C. | $\frac{13-4\sqrt{3}}{4}$ | D. | $\frac{15-5\sqrt{3}}{4}$ |
8.设函数f(x)=x(lnx-ax)(a∈R)在区间(0,2)上有两个极值点,则a的取值范围是( )
| A. | $(-\frac{1}{2},0)$ | B. | $(0,\frac{ln2+1}{4})$ | C. | $(\frac{1}{2},1)$ | D. | $(\frac{ln2+1}{4},\frac{1}{2})$ |
5.对于函数y=f(x),若存在区间[a,b],当x∈[a,b]时的值域为[ka,kb](k>0),则称y=f(x)为k倍值函数.若f(x)=lnx+x是k倍值函数,则实数k的取值范围是( )
| A. | $({0,1+\frac{1}{e}})$ | B. | $({1,1+\frac{1}{e}})$ | C. | (1,1+e) | D. | (1,1+e2) |
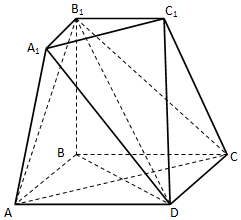 如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)
如图所示的几何体是由棱台ABC-A1B1C1和棱锥D-AA1C1C拼接而成的组合体,其底面四边形ABCD是边长为2的菱形,且∠BAD=60°,BB1⊥平面ABCD,BB1=2A1B1=2.(${V_{棱台}}=\frac{1}{3}h({{S_上}+{S_下}+\sqrt{{S_上}{S_下}}})$)